link zum pdf

In dieser Einheit geht es um das Erstellen von Tabellen mit freq und Grafiken mittels ggplot2. Durch ggplot2 erstellte Grafiken in R finden eine breite Verwendung in vielen akademischen und professionellen Feldern, in denen die Aufbereitung und Visualisierung von Daten und Statistiken gefordert ist. In der Lerneinheit wird mit den Daten aus dem Kurs gearbeitet, für die Übung mit dem European Social Survey.

# Statistik 1: R Tutorat
# Übungsskript zu univariaten Statistiken und Illustrationen
# Datum: 03.11.2024
# AutorIn: XXX

 

Vorbereitung: Aktivieren der nötigen Packages

#install.packages("tidyverse")
library(tidyverse)

 

0. Working Directory setzen

R speichert Grafiken und Tabellen an den Orten, auf die R zuletzt zugegriffen hat (z.B. Daten- oder Skriptordner). Das ist aber nicht immer erwünscht und führt zu unübersichtlichen Projektstrukturen. Mit der Festlegung einer Working Directory können wir in R-Studio definieren, in welchen Ordner R speichert.
Tipps:

# Daten einlesen
library(haven)
kursdata_anon <- read_dta("mein_laufwerk/mein_datenverzeichnis/kursdata_anon.dta")
# Working Directory für Grafiken etc definieren
setwd("mein_laufwerk/mein_Ergebnisverzeichnis")

# Alternativ: working directory setzen über Konsole:
# "Set Working Directory" --> "Choose Directory"
# working directory anzeigen lassen
getwd()

 

1. Tabellen mit R

1.1 Tabelle: Verteilung einer kategorialen Variable

Der Befehl freq() aus dem Package summarytools erzeugt eine Tabelle, aus der ihr direkt Anteile, kumulierte Prozente und absolute Werte ablesen könnt. Die validen Prozente geben die Prozentanteile der jeweiligen Kategorien ohne Einbezug der NA an. Achtung: Bei einigen Mac Usern wird für eine erfolgreiche Installation/Aktivierung des Summarytools-Packages der vorherige Download und Installation des XQuartz Programms benötigt. Der Downloadlink wird den Mac Usern in der Fehlermeldung hinterlegt. Alternativ findet man das Programm aber auch über Folgenden Link:https://www.xquartz.org/

Wir inspizieren zunächst die Variable intmig (Interesse an Migration und Integration) und stellen ihre Verteilung tabellarisch dar:

attributes(kursdata_anon$intmig)
## $label
## [1] "interesse: Migration und Integration"
## 
## $format.stata
## [1] "%9.0g"
## 
## $class
## [1] "haven_labelled" "vctrs_vctr"     "double"        
## 
## $labels
##      sehr     etwas gar nicht 
##         1         2         3
#install.packages("summarytools")
library(summarytools)
freq(kursdata_anon$intmig)
## Frequencies  
## 
##               Freq   % Valid   % Valid Cum.   % Total   % Total Cum.
## ----------- ------ --------- -------------- --------- --------------
##           1     31     57.41          57.41     57.41          57.41
##           2     22     40.74          98.15     40.74          98.15
##           3      1      1.85         100.00      1.85         100.00
##        <NA>      0                               0.00         100.00
##       Total     54    100.00         100.00    100.00         100.00

Meistens ist es sinnvoll, kategoriale Variablen vor Verwendung des freq() Befehls zu faktorisieren, damit die Ausprägungen in der Tabelle ersichtlich werden (dieser Effekt tritt allerdings nur dann ein, wenn (a) entsprechende Wertelabel in der Variable hinterlegt sind - was hier der Fall ist - und (b) die Faktorisierungsvariante as_factor() (mit Unterstrich) zur Klassenspezifikation verwendet wird).

kursdata_anon$intmig <- as_factor(kursdata_anon$intmig)
freq(kursdata_anon$intmig)
## Frequencies  
## 
##                   Freq   % Valid   % Valid Cum.   % Total   % Total Cum.
## --------------- ------ --------- -------------- --------- --------------
##            sehr     31     57.41          57.41     57.41          57.41
##           etwas     22     40.74          98.15     40.74          98.15
##       gar nicht      1      1.85         100.00      1.85         100.00
##            <NA>      0                               0.00         100.00
##           Total     54    100.00         100.00    100.00         100.00

Der freq() Befehl eignet sich für die tabellarische Darstellung von Variablen mit einer überschaubaren Anzahl Ausprägungen. Die mit freq() erstellten Tabellen sind jedoch nicht direkt publikationswürdig und müssen noch weiterverarbeitet werden. Dies erfolgt am besten in Word. Dazu schreibst du die per freq() generierte Tabelle in ein neues Objekt und speicherst dies als “html” File.

tab_intmig<-freq(kursdata_anon$intmig)
print(tab_intmig, method="browser", file="intmig.html")

Ein File namens “intmig.html” ist nun automatisch in der Working Directory abgespeichert (wenn du keine Working Directory gesetzt hast, wird das File entweder am Speicherort des Skripts oder einfach unter “Documents” abgespeichert). Dieses File kannst du nun in Word öffnen und dort die Tabelle publikationswürdig aufbereiten. Alternativ kann der Output-File direkt im .doc-Format angelegt werden (was manchmal etwas besser, machmal etwas schlechter formatierbare Tabellen produziert). Im print()-Befehl muss dazu das file()-Argument angepasst werden: file="intmig.doc"

Bei der Weiterverarbeitung bzw. externen Formatierung in Word ist zu achten auf:

  • Titel
  • Ggf. Fragestellung in Untertitel
  • Klare Zeilen- und Spaltennamen (Sprache konsistent Deutsch oder Englisch)
  • Quellenangabe der Daten
  • Kumulierte Prozente nur bei mindestens ordinalen Variablen
  • Ein oder Zwei Nachkommastellen
  • Totale Prozente werden in der Regel nicht ausgewiesen
  • Die Zeile ‘keine Angabe’ bzw. ‘NA’ wird manchmal weggelassen und stattdessen in der Note ein Zusatz angefügt: “an …[hier gesamte Samplegrösse einfügen] fehlende Werte: keine Angabe”

 

1.2 Tabelle: Verteilung einer metrischen Variablen

Manchmal kann es sinnvoll sein, auch die Verteilung einer metrischen Variable als Häufigkeitstabelle darzustellen. Dazu müssen wir die Variable allerdings meistens zuerst klassifizieren. Zwar gibt es bestimmte Regeln für solche Klassifizierungsgsprozesse (siehe unten), aber auch viele Freiheiten, die in Abhängigkeit der Verteilungseigenschaften und des Erkenntnisinteresses ausgestaltet werden müssen.

Exkurs: Klassifizieren und Kategorisieren

  • Wir fassen Werte einer metrischen Variable für die Tabellierung insbesondere dann zusammen, wenn viele Ausprägungen vorliegen. 10er oder kleinere Skalen dagegen werden häufig auch nicht-klassifiziert tabellarisch dargestellt. Wir fassen ebenfalls Werte zusammen, wenn wir Interesse an einem kategorialen Konzept (z.B. “Armut”) haben, dem eine metrische Skala (z.B. “Einkommen”) zugrunde liegt, oder wenn unser Interesse, wie im Beispiel unten, explizit auf Tendenzen ausgerichtet ist.

  • Beim Klassifizieren steht die Zusammenfassung von Ausgangswerten im Vordergrund. Sowohl das Konzept als auch das metrische Niveau bleiben dabei oft (letzteres in den Grenz- oder Mittelwerten) erhalten. Beispiel: Einkommen -> 0-2000 CHF; 2001-4000 CHF usw.

  • Bei der Kategorisierung steht die Bildung neuer Kategorien - oft auch ein neues Konzept - im Vordergrund. Die Metrik geht dabei fast immer verloren. Beispiel: Einkommen -> “Arm”; “nicht Arm”. Die Grenzen zwischen Kategorisieren und Klassifizieren sind fliessend. Oft werden die beiden Begriffe Synonym verwendet.

  • Die Klassen/Kategorien sollten geschlossen nach unten und oben, disjunkt, erschöpfend und möglichst gleich breit sein

Wir klassifizieren nun die Variable Lebenszufriedenheit (lezufr) und stellen sie anschliessend wiederum mit freq() tabellarisch dar:

kursdata_anon$lezufr_kls[kursdata_anon$lezufr >= 0 & kursdata_anon$lezufr <= 33] <- "unzufrieden" 
kursdata_anon$lezufr_kls[kursdata_anon$lezufr >= 34 & kursdata_anon$lezufr <= 66] <- "zufrieden"
kursdata_anon$lezufr_kls[kursdata_anon$lezufr >= 67] <-"sehr zufrieden"

freq(kursdata_anon$lezufr_kls)
## Frequencies  
## 
##                        Freq   % Valid   % Valid Cum.   % Total   % Total Cum.
## -------------------- ------ --------- -------------- --------- --------------
##       sehr zufrieden     36     67.92          67.92     66.67          66.67
##          unzufrieden      3      5.66          73.58      5.56          72.22
##            zufrieden     14     26.42         100.00     25.93          98.15
##                 <NA>      1                               1.85         100.00
##                Total     54    100.00         100.00    100.00         100.00

Zwei Drittel (67%) der Befragten aus dem Kurs stufen sich als ‘sehr zufrieden’ ein (mit Werten zwischen 67 und 100). Etwas weniger als ein Viertel (bzw. 25%) liegen im Bereich einer ‘zufriedenen’ Selbsteinschätzung. 8% der Befragten haben einen Wert zwischen 0 und 33 gewählt und sind daher als ‘unzufrieden’ klassifiziert (oder eher “kategorisiert”? Ist ein Grenzfall).

Problem: R ordnet die Kategorien einer Variable bei deren Neubildung nicht entsprechend der Skala der zugrunde liegenden Variable, sondern alphabetisch. Dadurch weicht die Reihung in der Tabelle nun unschön von der ordinalen Logik der klassifizierten Variable ab. Der Befehl factor(), bzw. dessen sub-Befehl levels=c(), kann hier Abhilfe schaffen: Hiermit können wir die Reihenfolge der Kategorien definieren.

kursdata_anon$lezufr_kls <- factor(kursdata_anon$lezufr_kls,
            levels = c("unzufrieden", "zufrieden", "sehr zufrieden"))
freq(kursdata_anon$lezufr_kls)
## Frequencies  
## 
##                        Freq   % Valid   % Valid Cum.   % Total   % Total Cum.
## -------------------- ------ --------- -------------- --------- --------------
##          unzufrieden      3      5.66           5.66      5.56           5.56
##            zufrieden     14     26.42          32.08     25.93          31.48
##       sehr zufrieden     36     67.92         100.00     66.67          98.15
##                 <NA>      1                               1.85         100.00
##                Total     54    100.00         100.00    100.00         100.00

Auch diese Tabelle speichern wir zur externen Weiterverarbeitung bzw. Formatierung:

tab_lekl<-freq(kursdata_anon$lezufr_kls)
print(tab_lekl, method="browser", file="lekl.html")

Zusammenfassend die Arbeitsschritte der Häufigkeitstabellen mit freq():

    1. Klassifikations- oder Kategorisierungsentscheidung (bei metrischen Variablen)
    1. Variable generieren (bei metrischen Variablen)
    1. Faktorisieren (wenn nötig)
    1. Ggf. Kategoriennamen festlegen
    1. Häufigkeitstabelle erstellen (mit freq)
    1. Häufigkeitstabelle speichern
    1. Häufigkeitstabelle formatieren (extern)

 

1.3 Tabellen: Verteilungseigenschaften metrischer Variablen – «Stichprobenstatistik»

Tabellen sind ebenfalls ein nützliches Vehikel, um die Parameter von Verteilungen mehrerer (metrischer) Variablen kompakt darzustellen. Hierfür ist z.B. das stargazer Package geeignet.

Wir erstellen einen Teildatensatz mit den darzustellenden Variablen. Wir wählen die metrischen Variablen lezufr, llezufr, leftright und alter aus dem Kursdatensatz aus.

library(dplyr)
kursdata_T <- select(kursdata_anon, lezufr, llezufr, leftright, alter)

Wir aktivieren stargazer() und führen den Befehl aus:

library(stargazer)
## 
## Please cite as:
##  Hlavac, Marek (2022). stargazer: Well-Formatted Regression and Summary Statistics Tables.
##  R package version 5.2.3. https://CRAN.R-project.org/package=stargazer
stargazer(as.data.frame(kursdata_T), median = TRUE, iqr = TRUE, type = "text",
          title = "Übersichtstabelle: Univariate Statistik", digits = 2)
## 
## Übersichtstabelle: Univariate Statistik
## ============================================================
## Statistic N  Mean  St. Dev. Min Pctl(25) Median Pctl(75) Max
## ------------------------------------------------------------
## lezufr    54 66.37  29.18   -99   61.5     71     80.8   98 
## llezufr   54 62.46  22.56    0    50.8    67.5     80    95 
## leftright 54 32.46  19.56    0     20      30      44    100
## alter     53 22.49   2.06   19     21      22      25    26 
## ------------------------------------------------------------

Mit stargazer() erstellte Tabellen unterscheiden sich grundlegend von den freq()-Tabellen. Die Variablen sind bei stargazer() in den Zeilen angesiedelt und die Parameter der Verteilungen, statt die Verteilungen selbst, werden kenntlich gemacht. Solche Übersichtstabellen dienen nicht nur der kompakten Darstellung von Übersichtsstatistiken, sondern können auch bei der Dateninspektion hilfreich sein: In unserem Beispiel hat sich z.B. ein unerwünschter, falsch codierter Wert eingeschlichen (-99), den wir im Rahmen dieser Datenbearbeitung bisher übersehen hatten. Wir rekodieren ihn getreu der Notation von R als NA:

kursdata_anon$lezufr[kursdata_anon$lezufr == -99] <- NA
summary(kursdata_anon$lezufr)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##   10.00   63.00   71.00   69.49   81.00   98.00       1

Wir führen nochmals denselben Befehl durch mit der bereinigten Variablen.

kursdata_T <- select(kursdata_anon, lezufr, llezufr, leftright, alter)
stargazer(as.data.frame(kursdata_T), median = TRUE, iqr = TRUE, type = "text",
          title = "Übersichtstabelle: Univariate Statistik", digits = 2)
## 
## Übersichtstabelle: Univariate Statistik
## ============================================================
## Statistic N  Mean  St. Dev. Min Pctl(25) Median Pctl(75) Max
## ------------------------------------------------------------
## lezufr    53 69.49  18.23   10     63      71      81    98 
## llezufr   54 62.46  22.56    0    50.8    67.5     80    95 
## leftright 54 32.46  19.56    0     20      30      44    100
## alter     53 22.49   2.06   19     21      22      25    26 
## ------------------------------------------------------------

Damit wir diese Tabelle aufbereiten können, speichern wir sie als Word-Dokument im html-Modus ab:

stargazer(as.data.frame(kursdata_T), median = TRUE, type = "html",iqr = TRUE, out = "stargazer.doc",
          title = "Übersichtstabelle: Univariate Statistik", digits = 2)

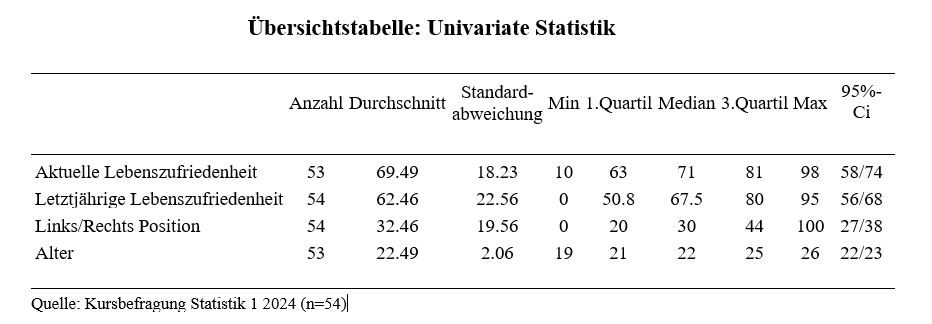
Ein File namens “stargazer.doc” ist jetzt in eurer Working Directory abgespeichert. Dieses File könnt ihr mit der Textverarbeitung öffnen und weiterbearbeiten. Neben der Formatierung könnten dort auch weitere statistische Parameter manuell zugefügt werden, wie die 95%-Konfidenzintervalle der Mittelwerte:

ci_lezufr <- t.test(kursdata_anon$lezufr)
ci_lezufr$conf.int

ci_llezufr <- t.test(kursdata_anon$llezufr)
ci_llezufr$conf.int

ci_leftright <- t.test(kursdata_anon$leftright)
ci_leftright$conf.int

ci_alter <- t.test(kursdata_anon$alter)
ci_alter$conf.int

Es gelten die gleichen Formatierungsstandards wie bei der Häufigkeitstabelle oben, letztlich sollte Eure Stichprobenstatistik bzw. Übersichtstabelle in etwa so aussehen:

 

2. Grafische Darstellung

2.0 Einführung

#install.packages("ggplot2")
library(ggplot2)

Wir erstellen Grafiken in R/ RStudio mit dem Package ggplot2. Dies ist ein weit verbreitetes Package mit einer grossen Auswahl an Gestaltungsmöglichkeiten. Startpunkt ist also die Installation und Aktivierung von ggplot2. Alternativ kann man auch das tidyverse Meta-Package aktivieren, da ggplot2 Teil davon ist. Hinweis: Die folgenden Befehlssequenzen dienen in erster Linie der didaktischen Motivation. Verwendet wird in der Praxis schliesslich immer nur die vollständige Plot-Funktion.

 

2.1 Barplot

Wir werden uns schrittweise an die Befehlslogik von Darstellungen anhand von ggplot2 heran tasten. Zuerst widmen wir uns der Darstellung kategorialer Variablen. An erster Stelle wird eine leere Grafikvorlage erstellt und der Datensatz bestimmt:

plot_1 <- ggplot(kursdata_anon)
plot_1

Mit aes() werden die relevanten Variablen aufgerufen. Da wir einen univariaten Plot erstellen, müssen wir nur eine Variable festlegen (hier:konsum). Die Kategorien der Variable sollen horizontal angeordnet sein, also die x-Achse definieren.

kursdata_anon$konsum<-as_factor(kursdata_anon$konsum)
plot_1 <- ggplot(kursdata_anon, aes(x = konsum))
plot_1

Hiermit ist die univariate Befehlsbasis bereits vollständig. Darauf folgen Zusätze, welche die Art, Beschriftung und Ästhetik der Darstellung ausmachen. Jeder Zusatz wird mit einem + an den Basisbefehl angehängt.
Mit den “geoms” wird die Art des Plots bestimmt. In diesem Fall steht das geom_bar für ein Säulendiagramm (= Barplot). Das ggplot2-Cheatsheet gibt einen Überblick zu den verschiedenen geom-Typen bzw. Abbildungsarten.

plot_1 <- ggplot(kursdata_anon, aes(x = konsum))+ 
  geom_bar()
plot_1

Innerhalb des jeweiligen geom() Zusatzes lassen sich weitere Elemente der Grafik spezifizieren, wie beispielsweise die Farbe, Breite oder Anzahl der Balken. Auch diesbezüglich findet ihr geom spezifische Informationen im Cheatsheet. Mit color bestimmen wird z.B. die Rahmenfarbe, mit fill die Füllfarbe der Balken.

plot_1 <- ggplot(kursdata_anon, aes(x = konsum))+ 
  geom_bar(colour = "blue", fill = "orange")
plot_1

Innerhalb von labs() können die Achsentitel und der Plottitel festgelegt werden, mit caption können zusätzliche Informationen unterhalb des Plots ergänzt werden.

plot_1 <- ggplot(kursdata_anon, aes(x = konsum))+ 
  geom_bar(colour = "blue", fill = "orange")+
  labs(x = "Supermarkt", y = "Anzahl", title = "Konsumpräferenz im Kurs",
       subtitle = "'Welchen Supermarkt bevorzugen Sie?'",
       caption ="Quelle: Kursbefragung Statistik I (n=...)")
plot_1

Mit theme kann der Hintergrund festgelegt werden: classic() steht in diesem Fall für einen transparenten/keinen Hintergrund.

plot_1 <-   ggplot(kursdata_anon, aes(x = konsum))+ 
  geom_bar(colour = "blue", fill = "orange")+
  labs(x = "Supermarkt", y = "Anzahl", title = "Konsumpräferenz im Kurs",
       subtitle = "'Welchen Supermarkt bevorzugen Sie?'",
       caption ="Quelle: Kursbefragung Statistik I (n=...)")+
  theme_classic()
plot_1

Im Barplot ist die Kategorie ‘keine Angabe’ enthalten. Diese Kategorie schliessen wir nun aus der Darstellung aus. Dazu müssen wir die Personen, die ‘keine Angabe’ gemacht haben, vorab ausfiltern und einen neuen, entsprechend reduzierten Datensatz erstellen. Wichtig: Fallzahl in der Caption anpassen!

library(dplyr)
kursdata_anon_N <- filter(kursdata_anon, konsum != "NA")

plot_1 <-   ggplot(kursdata_anon_N, aes(x = konsum))+ 
  geom_bar(colour = "blue", fill = "orange")+
  labs(x = "Supermarkt", y = "Anzahl", title = "Konsumpräferenz im Kurs",
       subtitle = "'Welchen Supermarkt bevorzugen Sie?'",
       caption ="Quelle: Kursbefragung Statistik I (n=...)")+
  theme_classic()
plot_1

Nun wollen wir die Kategorien auf der x-Achse umbenennen; die Namen der beiden Ketten sollen gross geschrieben werden.

plot_1 <-   ggplot(kursdata_anon_N, aes(x = konsum))+ 
  geom_bar(colour = "blue", fill = "orange")+
  scale_x_discrete(labels = c("Coop", "Migros"))+ 
  labs(x = "Supermarkt", y = "Anzahl", title = "Konsumpräferenz im Kurs",
       subtitle = "'Welchen Supermarkt bevorzugen Sie?'",
       caption ="Quelle: Kursbefragung Statistik I (n=...)")+
  theme_classic()
plot_1

In einem letzten Schritt wollen wir die Häufigkeiten auf der y-Achse als Anteile ausgeben. Mit aes(y = after_stat(count / sum(count))) werden die Häufigkeiten auf der y-Achse in Anteilswerte (0, 0.2, 0,4 etc.) umgewandelt. Innerhalb der Achsenspezifikation scale_y_continuous() kann dann die Ausgabe der Anteile über labels = scales::percent in Prozentwerten angefordert werden. Wir erhalten damit den fertigen Barplot.

plot_1 <-   ggplot(kursdata_anon_N, aes(x = konsum))+ 
  geom_bar(colour = "blue", fill = "orange")+
  scale_x_discrete(labels = c("Coop", "Migros"))+ 
  aes(y = after_stat(count / sum(count)))+ 
  scale_y_continuous(labels = scales::percent)+
  labs(x = "Supermarkt", y = "Anteil", title = "Konsumpräferenz im Kurs",
       subtitle = "'Welchen Supermarkt bevorzugen Sie?'",
       caption ="Quelle: Kursbefragung Statistik I (n=...)")+
  theme_classic()
plot_1

 

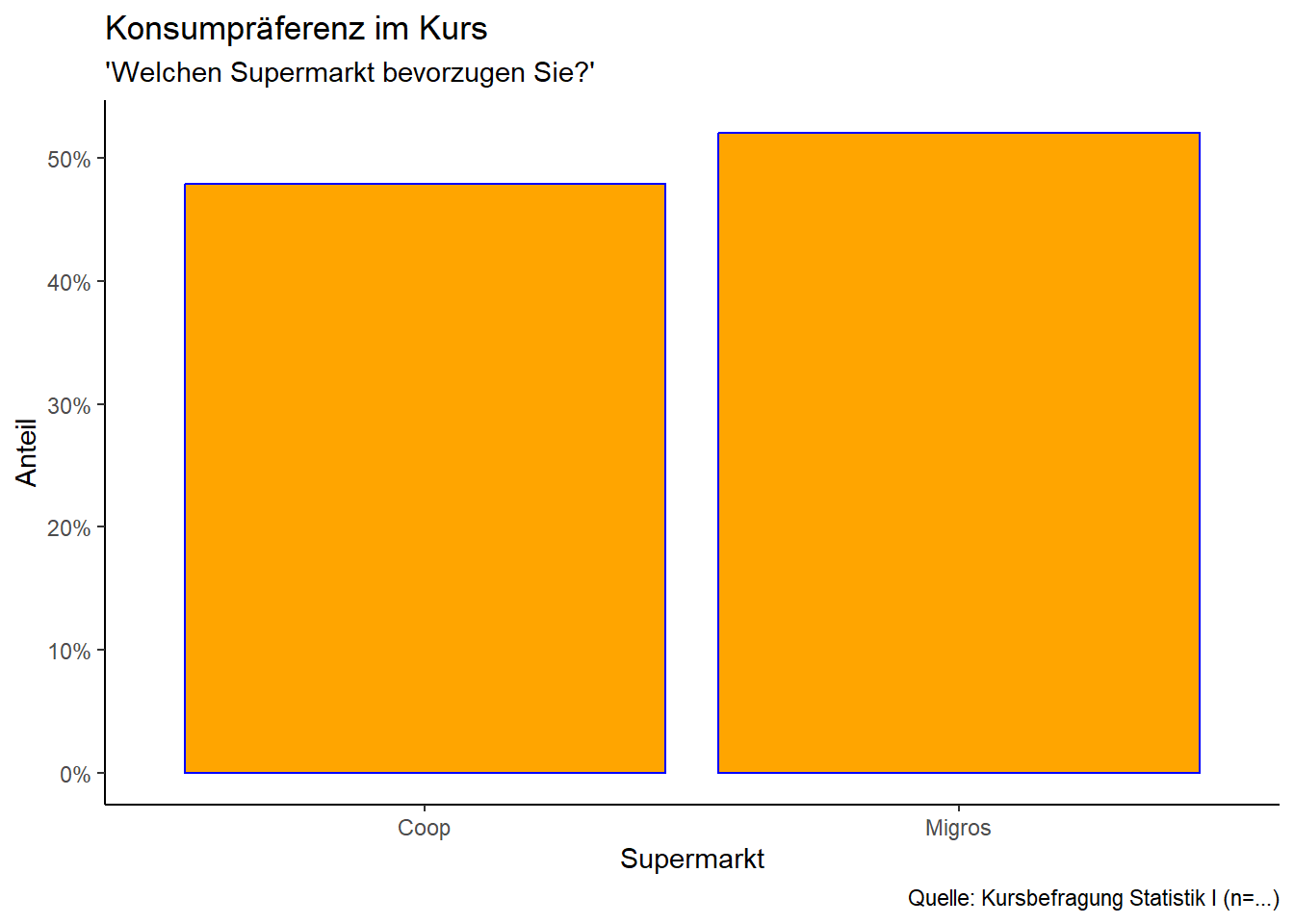
2.2 Histogramm

Histogramme sehen Barplots ähnlich, eignen sich jedoch für die Visualisierung von metrischen und kontinuierlichen Variablen mit vielen Ausprägungen. Wir erstellen ein Histogramm mithilfe eines neuen geom: geom_histogram() für die metrische Variable lezufr.

In einem ersten Schritt bereinigen wir die Variablen.

kursdata_anon$lezufr[kursdata_anon$lezufr == -99] <- NA

Der Befehl zur Erstellung eines Histogramms ist ähnlich dem Barplot-Befehl aufgebaut:

plot_2 <- ggplot(kursdata_anon, aes(x = lezufr))+ 
  geom_histogram (fill = "magenta", color="chocolate4", breaks = c(0,10,20,30,40,50,60,70,80,90,100))+
  labs(x = "Lebenszufriedenheit",y ="Anzahl", 
       title = "Lebenszufriedenheit in der Kursbefragung", 
       subtitle = "Wie zufrieden bist du mit deinem Leben auf einer Skala von 1 (gar nicht) bis 100 (sehr)?",
       caption = "Quelle: Kursbefragung Statistik I (n=...)")+ 
  scale_x_continuous(breaks = seq(0,100,10))+ 
  scale_y_continuous(breaks = seq(0,25,5))+ 
  theme_classic()
plot_2

Einige Aspekte müssen jedoch verändert werden.

  • aes(x = lezufr): Wir erzeugen weiterhin einen univariaten Plot und müssen deshalb nur eine Variable bestimmen. Wir nehmen nun aber eine metrische Variable, die Lebenszufriedenheit der Kursteilnehmenden.

  • geom_histogram(): Da jetzt ein Histogramm erzeugt werden soll, müssen wir den Befehl für die Art des Plots ändern.

    • breaks =: Hier kann die Anzahl und die Breite der Säulen und ihre Grenzen bestimmt werden. In diesem Beispiel schliesst die erste Säule Werte von (0)-(9) ein, die zweite von (10)-(19) etc. Mit c() werden die einzelnen Grenzen manuell bestimmt. Alternativ könnten mit seq(0,100,10) automatisiert 10er Schritte von (0) bis (100) befohlen werden.

    • bins =: Anstatt breaks. Hier kann die Anzahl der Säulen bestimmt werden. bins = 20 würde 20 Säulen anzeigen.

    • binwidth =: Anstatt bins. Hier kann die Breite der Säulen festgelegt werden. binwidth = 5 würde eine Säulenbreite von 5 heissen. Das heisst die erste Säule wäre von (0)-(5), die zweite von (5)-(10) etc.

  • scale_x_continuous(): Mit diesem Argument kann das Skalenniveau für die x-Achse bestimmt werden. In diesem Fall von 0 bis 100 in 10er Schritten.

  • scale_y_continuous(): Mit diesem Argument kann das Skalenniveau für die y-Achse bestimmt werden. In diesem Fall von 0 bis 20 in 1er Schritten.

  • breaks = seq(): Mit diesem Argument können wir das untere und das obere Limit für die beiden Achsen festlegen. Ausserdem können wir den Abstand auf den Achsen zwischen zwei Punktbeschriftungen festlegen.

 

2.3 Boxplot

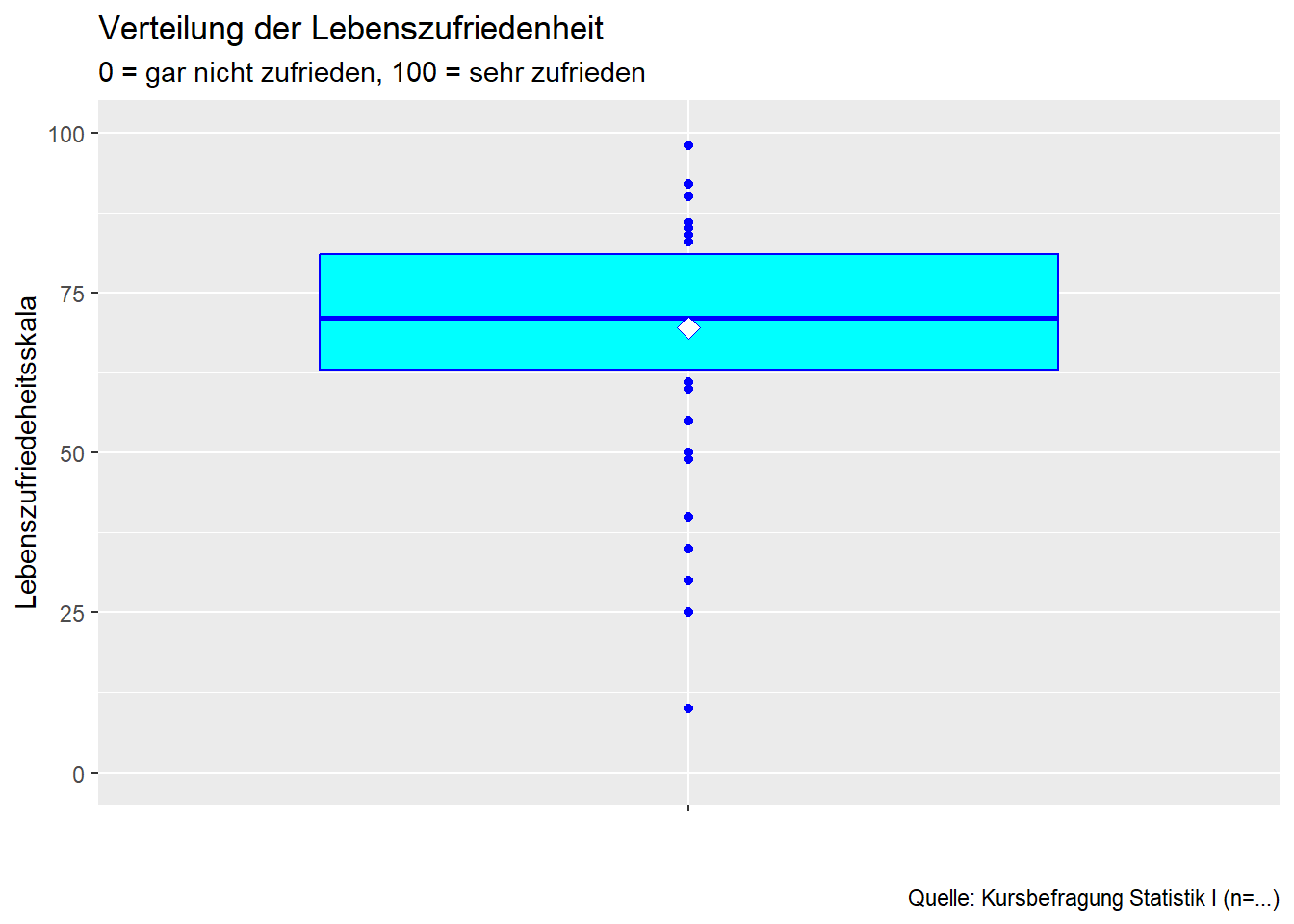
Boxplots stellen ebenfalls eine Möglichkeit dar, um Verteilungen metrischer Variablen zu visualisieren. Allerdings werden hierbei nicht die Verteilungen selbst, sondern deren Parameter grafisch dargestellt: Jede der drei Linien des Boxplots steht für ein Quartil der Fälle, also Q1=25%, Q2=50% und Q3=75%. Der Median, bzw. Q2, wird als dicke Linie in der Mitte der Box hervorgehoben. Dementsprechend umfasst die Höhe der Box den Interquartilsabstand “IQR”. Wir gewöhnen uns an, zusätzlich per Raute den Mittelwert der Verteilung kenntlich zu machen.

Der folgende Boxplot soll die Verteilung der Lebenszufriedenheit im Kurs zeigen.

Wir erarbeiten den Befehl zur Erstellung des Plots wieder schrittweise:
Wir erstellen eine leere Grafik und reichern sie mit der metrischen Variablen lezufr auf der y-Achse an, da die Verteilung in Boxplots normalerweise vertikal dargestellt wird.

plot_3 <- ggplot(kursdata_anon, aes(y = lezufr))
plot_3

Die Diagrammart geom_boxplot und die Farben werden bestimmt. Mit coef=0 werden die Linien ober und unterhalb des Boxplots eleminiert, die jeweils das das 1,5-Fache des IQR messen und insbesondere zur kompakten Darstellung bei Daten mit vielen Messpunkten sinnvoll sind.

plot_3 <- ggplot(kursdata_anon, aes(y = lezufr))+ 
  geom_boxplot(colour = "blue", fill = "cyan", coef=0)
plot_3

Die “Range” der y-Achse wird mit ylim(0,100) bestimmt. So kann die y-Achse erweitert werden, damit nicht nur der empirisch realisierte Bereich abgebildet wird. In unserem Beispiel gibt es Leute mit Lebenszufriedenheit (0) aber auch (100). Das heisst die Range ist maximal. Es hätte jedoch auch sein können, dass niemand eine Lebenszufriedenheit unter (30) angegeben hat. Dann würde die Skala auf der y-Achse bei 30 enden. Mit ylim(0,100) könnten wir sie trotzdem bis 0 ziehen und somit den ganzen theoretischen Wertebereich der Variable lezufr anzeigen. Mit labs() werden wie gewohnt Beschriftungen vorgenommen.

plot_3 <- ggplot(kursdata_anon, aes(y = lezufr))+ 
  geom_boxplot(colour = "blue", fill = "cyan", coef=0)+ 
  ylim(0,100) + 
  labs(y = "Lebenszufriedeheitsskala",
       title = "Verteilung der Lebenszufriedenheit",
       subtitle = "0 = gar nicht zufrieden, 100 = sehr zufrieden",
       caption = "Quelle: Kursbefragung Statistik I (n=...)")
plot_3

Die x-Achse ist im Falle einer univariaten Verteilung mit einem Boxplot nicht von Bedeutung. Wir entfernen also die Beschriftung der x-Achse über labs und die Skala über aes.

plot_3 <- ggplot(kursdata_anon, aes(x = "",y = lezufr))+ 
  geom_boxplot(colour = "blue", fill = "cyan", coef=0) +
  ylim(0,100)+ 
  labs(y = "Lebenszufriedeheitsskala", x = "",
       title = "Verteilung der Lebenszufriedenheit",
       subtitle = "0 = gar nicht zufrieden, 100 = sehr zufrieden",
       caption = "Quelle: Kursbefragung Statistik I (n=...)")
plot_3

Schlussendlich wollen wir ein Rauten-Symbol für den Mittelwert/mean einfügen. Dafür benutzen wir stat_summary, über welchen wir Wert, Form und Farbe der Raute definieren können.

plot_3 <- ggplot(kursdata_anon, aes(x = "",y = lezufr))+ 
  geom_boxplot(colour = "blue", fill = "cyan", coef=0) +
  ylim(0,100)+ 
  labs(y = "Lebenszufriedeheitsskala", x = "",
       title = "Verteilung der Lebenszufriedenheit",
       subtitle = "0 = gar nicht zufrieden, 100 = sehr zufrieden",
       caption = "Quelle: Kursbefragung Statistik I (n=...)") +
  stat_summary(fun=mean, geom="point", shape=23, size=3, color="blue", fill="white")
plot_3

 

3. Export von Grafiken

Möglichkeit 1: Die quick & dirty “in 15 Minuten beginnt der Vortrag”-Variante

Du kannst die zuletzt aufgerufene Grafik im R-Studio Fenster unten rechts (unter “Plots”) durch manuelles Verschieben von Fenstergrösse und -verhältnis so kalibrieren, dass Seitenabmessung, Schriftgrösse etc. stimmig sind. Nun kannst du den Graph per rechtsklick kopieren (oder mit einem Bildschirmausschnitt, zweckmässig über ein Snippet Tool o.ä., die Grafik ausschneiden) und in eine Präsentation oder sonstigen File einfügen. Das Ergebnis ist für präsentationszwecke meist ok. Für die Einbindung in schriftliche Dokumente, Poster etc ist diese Variante aufgrund der mittelmässigen Qualität und fehlender Replizierbarkeit gleichwohl nicht geeignet.

Möglichkeit 2: Skriptbasiert mit dem generischen R-Grafiktreiber

Alternativ können die Grafiken über das Skript exportiert werden. Die Grafik wird dann automatisch in dem als working directory definierten Ordner abgespeichert.

png("boxplot.png", width = 12, height = 12, units = "cm", res = 300)          
plot(plot_3)
dev.off()
pdf("boxplot.pdf")          
plot(plot_3)
dev.off()

Auf diese Weise können verschiedene Grafikformate realisiert werden - im Beispielcode oben wurde die Abbildung sowohl im .png-Format als auch als pdf angelegt. Diese Formate sind je nach Anwendungskontext und Grafikvorgaben mal mehr, mal weniger geeignet. pdf() kreiert auflösungsunabhängige Vektorgrafiken, was oft attraktiv ist, manchmal aber auch nicht funktioniert. png() funktioniert dagegen fast immer, erzeugt aber extrem grosse Dateien wenn die Auflösung z.B. für eine Postergrafik hinreichend sein soll.

In keinem der gängigen Speicherformate bleibt es nach unserer Erfahrung aus, sich schrittweise zur optimalen Kombination von Exportkonfiguration und ggf. auch Schriftgrösseneinstellungen im ggplot-Befehl vorzuarbeiten.

Möglichkeit 3: Skriptbasiert mit ggsave()

Letzter Punkt gilt grundsätzlich auch für die dritte Exportvariante. Das Kommando ggsave() ist spezifisch auf ggplot()-produzierte Grafiken ausgerichtet und lässt sich dann oft komfortabler nutzen als die generischen R-Grafiktreiber. Möglicherweise nutzt es häufig einen sinnvollen Grössen-, Auflösungs- und Seitenverhältnisdefault beim Speichern von Grafiken ohne dezidierte Spezifikation - darauf würde ich mich aber nicht verlassen und lieber stets die Konfiguration selbst anpassen. Auch ggsave() kann in verschiedene Formate exportieren.

ggsave(filename = "boxplot_ggsave1.png", plot=plot_3) ## Defaulteinstellung generiert Abbildung, die OK ist.         
ggsave(filename = "boxplot_ggsave2.png", plot=plot_3, height=10, width=10, units = "cm", dpi = 600) ## Auflösung wurde höher gesetzt, zudem Abmessungen so angepasst, dass Schrift grösser ist.
ggsave(filename = "boxplot_ggsave3.png", plot=plot_3, height=5, width=5, units = "cm", dpi = 600) ## Beispiel: Schriftgrösse passt nicht mehr, muss ggf. im ggplot angepasst werden
ggsave(filename = "boxplot_ggsave4.png", plot=plot_3, height=40, width=40, units = "cm", dpi = 600) ## Beispiel2: Schriftgrösse passt nicht mehr, muss ggf. im ggplot angepasst werden (siehe unten)

ggsave(filename = "boxplot_ggsave3.pdf", height=4, width=4) ## Bei Verwendung von pdf als Output fällt wegen Vektorgrafik die Konfiguration der Auflösung weg. Gleichwohl ist es schwierig, pdf-Abbildungen in Powerpoint oder Word zu importieren.
# Plot mit angepasster Schriftgrösse (Kompatibel zu ggsave mit height=40 und width=40: "boxplot_ggsave4")
plot_3 <- ggplot(kursdata_anon, aes(x = "", y = lezufr)) + 
  geom_boxplot(colour = "blue", fill = "cyan", coef = 0, outlier.size = 4) +
  ylim(0, 100) + 
  labs(
    y = "Lebenszufriedeheitsskala", 
    x = "",
    title = "Verteilung der Lebenszufriedenheit",
    subtitle = "0 = gar nicht zufrieden, 100 = sehr zufrieden",
    caption = "Quelle: Kursbefragung Statistik I (n=...)"
  ) +
  stat_summary(fun = mean, geom = "point", shape = 23, size = 10, color = "blue", fill = "white") +
  theme(
    plot.title = element_text(size = 58),
    plot.subtitle = element_text(size = 32),
    axis.title.y = element_text(size = 32),
    axis.text.y = element_text(size = 32),
    plot.caption = element_text(size = 32)
  )

 

Hier gehts weiter zur Übung III