Beispielhaft beschäftigen wir uns in dieser Lerneinheit mit der
Frage, wie Bildung die Einstellung zur Migration beeinflusst. Da
Bildungsinstitutionen neben formalen Kompetenzen auch Werte wie
Offenheit und Toleranz vermitteln, formulieren wir als
Forschungshypothese: Bildung hat einen positiven Einfluss
auf Einstellungen zur Migration.
Wir steigen mit dem Datenmanagement, der Variablensuche und der
Dateninspektion ein - typische Arbeitsschritte vor dem Einstieg in jede
bi- oder multivariate Analyse.
Die grundlegenden Befehle zur Regressionsanalyse sind im Base R
vorinstalliert. Die im tidyverse Package enthaltenen
Befehle (dazu gehören auch die Befehle des dplyr und
des ggplot2) verwenden wir insbesondere im Zuge des
Datenmanagements sowie zur visualisierung. Erst im Rahmen der multiplen
Regressionsanalyse, im zweiten Teil des Semesters, benötigen wir
Packages, die über die Standardausstattung Base +
tidyverse hinausgehen.
1.2 Selektieren von Merkmalen
In einem zweiten Schritt bietet es sich an, den Datensatz auf die
relevanten Variablen zu reduzieren. Wir müssen aber zunächst die
Variablen identifizieren, welche zu unseren Konzepten Bildung
und Einstellungen zur Migration passen. Die Variablensuche
können wir entweder datensatzbezogen organisieren (mit den Befehlen
look_for() oder contents, siehe
Lerneinheit Basics), oder auf Grundlage des Codebook
zum ESS8 bzw. der online
Dokumentation des ESS durchführen.
Wir finden in diesem Fall jeweils mehrere Variablen vor, welche zu
den Konzepten passen. In der wissenschaftlichen Praxis hinge es nun von
unseren theoretischen Überlegungen und vom Forschungsstand ab, mit
welchen dieser Variablen wir arbeiten. Hier verwenden wir aus
didaktischen Gründen die Variablen eduyrs und
imueclt.
ess8_CH_ss <- select(ess8_CH, idno, eduyrs, imueclt)
Mithilfe des select()-Befehls aus dem
dplyr-Package lässt sich ein entsprechend reduziertes
Subset “ess8_CH_ss” aus dem Schweizer Teildatensatz bilden.
Der hier gebildete Teildatensatz enthält weiterhin 1525 Personen aus
der Schweiz, jedoch wurde die Anzahl Merkmale von 534 auf 3
reduziert.
1.3 Inspektion der Daten
In einem dritten Schritt inspizieren wir die ausgewählten Variablen.
Besonderes Augenmerk liegt auf der Ermittlung der Skalierung, der
Bedeutung der einzelnen Ausprägungen, univariaten Kennwerten, und der
Anzahl und Kodierung der Missings.
attributes(ess8_CH_ss$eduyrs)
## $label
## [1] "Years of full-time education completed"
##
## $format.stata
## [1] "%12.0g"
##
## $labels
## Refusal Don't know No answer
## NA NA NA
##
## $class
## [1] "haven_labelled" "vctrs_vctr" "double"
summary(ess8_CH_ss$eduyrs)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.0 9.0 10.0 11.3 13.0 26.0 3
hist (ess8_CH_ss$eduyrs)

sd(ess8_CH_ss$eduyrs, na.rm = TRUE)
## [1] 3.496909
attributes(ess8_CH_ss$imueclt)
## $label
## [1] "Country's cultural life undermined or enriched by immigrants"
##
## $format.stata
## [1] "%24.0g"
##
## $labels
## Cultural life undermined 1 2
## 0 1 2
## 3 4 5
## 3 4 5
## 6 7 8
## 6 7 8
## 9 Cultural life enriched Refusal
## 9 10 NA
## Don't know No answer
## NA NA
##
## $class
## [1] "haven_labelled" "vctrs_vctr" "double"
summary(ess8_CH_ss$imueclt)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.000 5.000 6.000 6.072 8.000 10.000 14
hist (ess8_CH_ss$imueclt)

barplot (table(ess8_CH_ss$imueclt))
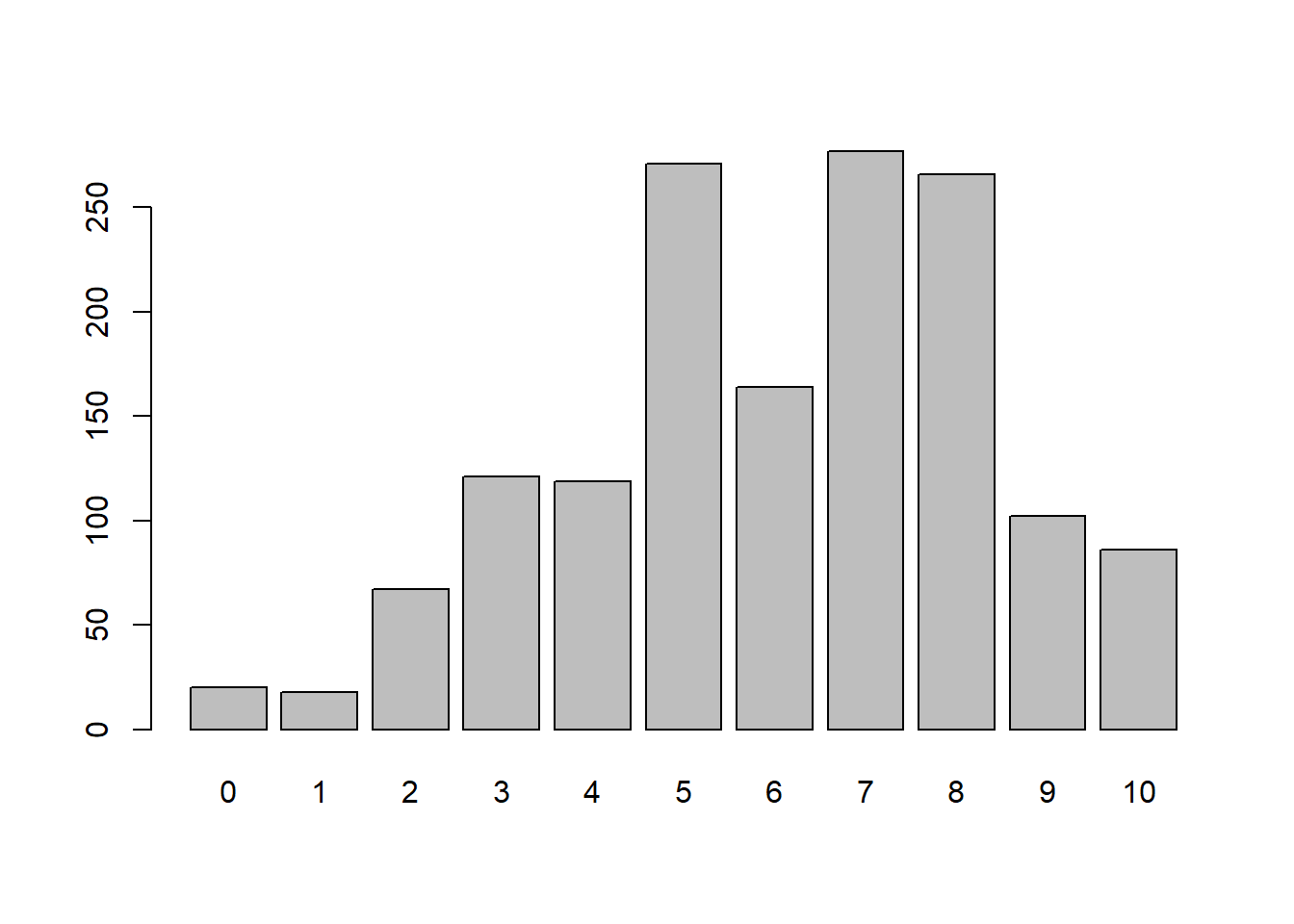
sd(ess8_CH_ss$imueclt, na.rm = TRUE)
## [1] 2.258924
Anhand des summary()-Befehls (und einem Abgleich mit
dem Codebook/attributes()-Befehl) können wir
kontrollieren, ob die Variablen korrekt codiert sind. Die
Bildungsvariable eduyrs wird anhand der abgeschlossenen
Bildungsjahre bemessen mit einem Minimum von 0 und einem Maximum von 26
Bildungsjahren. In unserem Datensatz schliessen SchweizerInnen im
Durchschnitt circa 11 Bildungsjahre ab.
Die Variable imueclt bezieht sich auf die kulturelle
Wertschätzung von Migration. Hohe Werte bedeuten hier, dass Migration
positive Einflüsse für das kulturelle Leben zugeschrieben werden,
während tiefere Werte für eine geringe kulturelle Wertschätzung von
Migration stehen. Mit dem attributes()-Befehl können
wir überprüfen, wie die Variable kodiert ist. Dem Wert 0 und 10 sind
jeweils konkrete Labels zugeordnet, wärend die werte dazwischen jeweils
nur mit einem Zahlenlabel versehen sind. Im Mittel tendieren
SchweizerInnen zu einer Einschätzung leicht oberhalb des Skalenmittels,
was am Mittelwert von 6.07 erkennbar ist.
Beide Merkmale enthalten keine Werte die rekodiert werden müssten. Es
gibt zudem wenig NAs - wären es viele (Daumenregel >10%), müsste dies
im Rahmen der Auswertung explizit berichtet oder begründet werden.
Gelegentlich wird dann auch auf eine alternative Variable ausgewichen.
Dieses ist aber im vorliegenden Fall, aufgrund der eben berichteten
geringen Anzahl fehlender Werte in den beteiligten Variablen, nicht
notwendig.
1.4 Visuelle Inspektion des Zusammenhangs im Streudiagramm
ggplot(ess8_CH_ss,
aes(x = eduyrs, y = imueclt)) +
geom_point()+
theme_bw()
## Warning: Removed 16 rows containing missing values or values outside the scale range
## (`geom_point()`).

Grundlage der Regressionsanalyse ist die Visualisierung des
Zusammenhangs im Streudiagramm. Dafür bietet sich der
ggplot()-Befehl aus dem
ggplot2-Package an. Die Merkmalsträger (bzw. deren
Ausprägungen) werden im Streudiagramm über einzelne Punkte
repräsentiert, die mit dem geom_point()-Teilbefehl
aktiviert werden. Achtet dabei auf die Belegung der x und y Achse. Das
unabhängige Merkmal (eduyrs) wird auf die x und das
abhängige Merkmal (imueclt) wird auf die y-Achse
gesetzt. Beachte, dass du deine Darstellung immer über
labs() vollständig beschriftest. Das bedeutet:
- Du hast einen klaren Titel, in dem entweder die Konzepte oder
einfache Beschreibungen der Indikatoren aufgegriffen werden
- Die Frageformulierung der AV ggf. in den Untertitel
- Die Achsenbeschriftung ist aussagekräftig
- Die Achsengestaltung ist sinnvoll: Hinreichend viele Ticks &
Label sind gesetzt, aber keine unsinnigen (z.B. Dezimalstellen bei
Skalenvariablen)
- Du hast eine Fussnote, auf der du die Datenquelle und die
(Teil)Stichprobengrösse angibst - diese lässt sich leicht aus
Datensatzgrösse minus in der Warnung ggf. ausgewiesenen fehlenden Werten
ableiten.
ggplot(ess8_CH_ss, aes(x = eduyrs, y = imueclt)) +
geom_point() +
scale_x_continuous(breaks = seq(0, 26, 2)) +
scale_y_continuous(breaks = seq(0, 10, 1)) +
labs(
title = "Streudiagramm: Einstellung zur Migration nach Bildung",
subtitle = "Das kulturelle Leben wird durch Migration untergraben(0) oder bereichert(10)",
x = "Bildungsjahre",
y = "Migrationswertschätzung",
caption = "Daten ESS8(2016), Teilstichprobe CH(N=1509)"
) +
theme_bw() +
theme(plot.subtitle = element_text(face = "italic"))
## Warning: Removed 16 rows containing missing values or values outside the scale range
## (`geom_point()`).

Lässt sich bereits ein Trend ablesen? Gibt es Bedarf/Möglichkeiten,
die Grafik zugänglicher zu machen?
Ein klassisches Problem im Umgang mit diskret skalierten Variablen
und grossen Stichproben ist das “Overplotting”. Dabei liegen Punkte zu
dicht beieinander oder sogar, wie in diesem Fall, übereinander, wodurch
sich eine Interpretation der Grafik in vielen Fällen verkompliziert,
bzw. die visuelle Zugänglichkeit des dargestellten Zusammenhangs
deutlich eingeschränkt ist. Zur Lösung dieses Problem bietet
das ggplot2-Package eine Vielzahl von
Möglichkeiten:
1.4.1 Streudiagramm mit transparenten Punkten
ggplot(ess8_CH_ss, aes(x = eduyrs, y = imueclt)) +
scale_x_continuous(breaks = seq(0,26,2)) +
scale_y_continuous(breaks = seq(0,10,1)) +
geom_point(alpha = 0.1, size = 4)+
labs(
title = "Streudiagramm: Einstellung zur Migration nach Bildung",
subtitle = "Das kulturelle Leben wird durch Migration untergraben(0) oder bereichert(10)",
x = "Bildungsjahre",
y = "Migrationswertschätzung",
caption = "Daten ESS8(2016), Teilstichprobe CH(N=1509)"
) +
theme_bw() +
theme(plot.subtitle = element_text(face = "italic"))

Eine einfache Lösung des Overplotting ist es, die Messpunkte
transparent (alpha=0: völlig
durchsichtig, alpha=1: voll
deckend) abzubilden. Die Farbtiefe der Punkte lässt so auf die
Belegungsdichte der einzelnen Merkmalskombinationen schliessen.
Zusätzlich erhöhen wir die Grösse der Punkte (alpha und
size können in allen geom_-Befehlen
spezifiziert werden). Achtung: Die sinnvolle
Spezifikation von alpha und size hängt
immer von den Eigenheiten der Stichprobe und der Messskalen ab.
Grundlegend zur Optimierung der visuellen Kraft gilt: Je grösser die
Stichprobe, desto stärker sollte die Transparenz der einzelnen Punkte
gewählt werden und je gröber die Skalen, desto grösser können die Punkte
dargestellt werden. Ohne Ausprobieren geht es nicht - experimentiert
also immmer mit der Konfiguration und fragt euch dabei, mit welcher
Spezifikation die zentrale Botschaft zur gemeinsamen Verteilung (bzw.
zum Zusammenhang) am ausdruckstärksten transportiert wird.
1.4.2 Jitter-Plot
ggplot(ess8_CH_ss, aes(x = eduyrs, y = imueclt)) +
scale_x_continuous(breaks = seq(0,26,2)) +
scale_y_continuous(breaks = seq(0,10,1)) +
geom_jitter()+
labs(
title = "Streudiagramm (Jitter): Einstellung zur Migration nach Bildung",
subtitle = "Das kulturelle Leben wird durch Migration untergraben(0) oder bereichert(10)",
x = "Bildungsjahre",
y = "Migrationswertschätzung",
caption = "Daten ESS8(2016), Teilstichprobe CH(N=1509)"
) +
theme_bw() +
theme(plot.subtitle = element_text(face = "italic"))

Mit dem Befehl geom_jitter() werden die Messpunkte
jeweils leicht in eine zufällige Richtung verschoben. Dadurch liegen
Punkte mit gleicher Merkmalskombination nicht mehr perfekt übereinander
und werden so einzeln sichtbar gemacht. Die Funktionalität ist
insbesondere dann sinnvoll, wenn eine oder beide Variablen über (grobe)
Skalen gemessen wurden. Über height und
width können wir angeben, wie stark die Punkte zufällig
streuen sollen:
ggplot(ess8_CH_ss, aes(x = eduyrs, y = imueclt)) +
scale_x_continuous(breaks = seq(0,26,2)) +
scale_y_continuous(breaks = seq(0,10,1)) +
geom_jitter(height= 2, width = 2)+
labs(
title = "Streudiagramm (Jitter): Einstellung zur Migration nach Bildung",
subtitle = "Das kulturelle Leben wird durch Migration untergraben(0) oder bereichert(10)",
x = "Bildungsjahre",
y = "Migrationswertschätzung",
caption = "Daten ESS8(2016), Teilstichprobe CH(N=1509)"
) +
theme_bw() +
theme(plot.subtitle = element_text(face = "italic"))

Hier wurde unnötig viel Streuung zugesetzt, so dass nun z.B. die
Streuungseigenschaften der beiden Variablen stark verfremdet abgebildet
werden, ohne dass dabei die Ausdruckskraft zum Zusammenhang gesteigert
werden konnte. Jitter also immer nach Prinzip “so viel wie nötig, so
wenig wie möglich” einsetzen.
Zuletzt können wir auch in diesem Befehl alpha und
size anpassen:
ggplot(ess8_CH_ss, aes(x = eduyrs, y = imueclt)) +
scale_x_continuous(breaks = seq(0,26,2)) +
scale_y_continuous(breaks = seq(0,10,1)) +
geom_jitter(alpha = 0.2, size = 3)+
labs(
title = "Streudiagramm (Jitter): Einstellung zur Migration nach Bildung",
subtitle = "Das kulturelle Leben wird durch Migration untergraben(0) oder bereichert(10)",
x = "Bildungsjahre",
y = "Migrationswertschätzung",
caption = "Daten ESS8(2016), Teilstichprobe CH(N=1509)"
) +
theme_bw() +
theme(plot.subtitle = element_text(face = "italic"))

Dank der grösseren Punkte und deren Transparenz zeichnet sich nun
besser eine positive Korrelation zwischen den beiden Variablen ab.
Aufgrund der sich bei Zunahme der Bildungsjahre (Trend nach rechts) nach
oben verschiebende Unterkante der Verteilung ergibt sich durch die
Visualisierung ein substantzieller Einblick in die Natur des
Zusammenhangs: mit zunehmenden Bildungsniveau dünnen die niedrigen
Wertschätzungen für Migration aus.
1.4.3 Heatmaps
ggplot(ess8_CH_ss, aes(x = eduyrs, y = imueclt)) +
scale_x_continuous(breaks = seq(0,26,2)) +
scale_y_continuous(breaks = seq(0,10,1)) +
geom_bin2d() +
labs(
title = "Heatmap: Einstellung zur Migration nach Bildung",
subtitle = "Das kulturelle Leben wird durch Migration untergraben(0) oder bereichert(10)",
x = "Bildungsjahre",
y = "Migrationswertschätzung",
caption = "Daten ESS8(2016), Teilstichprobe CH(N=1509)"
) +
theme_bw() +
theme(plot.subtitle = element_text(face = "italic"))

Mit dem Befehl geom_bin_2d() können wir Heatmaps
generieren. Dabei wird die Belegungsdichte in verschiedenen Regionen der
gemeinsamen Verteilung über die farbliche Tiefe des jeweiligen Segmentes
dargestellt.
Naja, wirklich hilfreich ist diese Darstellung so noch nicht. Die Map
ist zerstückelt und die Verwendung der Farben ist nicht intuitiv. Wenn
wir Heatmaps erstellen, sollten 1. möglichst keine Lücken zwischen den
Felder vorhanden sein und 2. sollte eine hohe Belegung der Felder immer
durch eine dunklere Farbe gekennzeichnet sein. Ersteres können wir durch
das anpassen der bins im
geom_bin2d()-Befehl erreichen.
ggplot(ess8_CH_ss, aes(x = eduyrs, y = imueclt)) +
scale_x_continuous(breaks = seq(0,26,2)) +
scale_y_continuous(breaks = seq(0,10,1)) +
geom_bin2d(bins =9) +
labs(
title = "Heatmap: Einstellung zur Migration nach Bildung",
subtitle = "Das kulturelle Leben wird durch Migration untergraben(0) oder bereichert(10)",
x = "Bildungsjahre",
y = "Migrationswertschätzung",
caption = "Daten ESS8(2016), Teilstichprobe CH(N=1509)"
) +
theme_bw() +
theme(plot.subtitle = element_text(face = "italic"))

Sieht doch schon viel besser aus, aber die Farben stimmen immer noch
nicht. Dies können wir nun über den Befehl
scale_fill_gradient() anpassen. Hier können wir auch
jegliche Farben verwenden, die uns passen (eine Übersicht der Farben
findest du Hier).
ggplot(ess8_CH_ss, aes(x = eduyrs, y = imueclt)) +
scale_x_continuous(breaks = seq(0,26,2)) +
scale_y_continuous(breaks = seq(0,10,1)) +
geom_bin2d(bins =9) +
scale_fill_gradient(low = "lavenderblush",
high = "red") +
labs(
title = "Heatmap: Einstellung zur Migration nach Bildung",
subtitle = "Das kulturelle Leben wird durch Migration untergraben(0) oder bereichert(10)",
x = "Bildungsjahre",
y = "Migrationswertschätzung",
caption = "Daten ESS8(2016), Teilstichprobe CH(N=1509)"
) +
theme_bw() +
theme(plot.subtitle = element_text(face = "italic"))

In diesem Fall lässt eine Heatmap nicht wirklich eine bessere
Interpretation des bivariaten Zusammenhangs zu. Sie ist hier daher auch
nicht das Visualisierungsinstrument erster Wahl. Insbesondere aber bei
sehr grossen Stichproben und groben Skalen, wenn selbst
Transparenzoptionen und jittern einer punktbasierten Visualisierung
nicht zur Ausdrucksstärke verhelfen, entfaltet die Heatmap oft ihre
Stärken.
1.4.4 Overplotting: Welche Lösung in welcher Situation?
Du siehst: es gibt verschiedene Lösungen für das Overplotting. Im
konkreten empirischen Fall wendest du diejenige an, welche die Beziehung
zwischen den Variablen am deutlichsten ausdrückt. Rezepthafte
Entscheidungsvorgaben zur Auswahl des Plots sind dabei nicht möglich:
Die Aussagekraft hängt oft von detaillierten Spezifika der Datenlage ab.
Zudem sind die Auswahlmöglichkeiten oft durch generelle Layout- oder
Satzvorgaben limitiert (viele Journals akzeptieren z.B. nur
S/W-Abbildungen). Es gibt aber allgemeine Leitbilder zur
Datenvisualisierung, aus denen sich ein paar Empfehlungen und Erwägungen
fürs Streudiagramm ableiten lassen:
Less is more: Wenn ein einfaches Streudiagramm funktioniert,
sollte dies auch verwendet werden
Die Transparenzoption ist minimal-invasiv und daher immer erste
Alternative. Insbesondere bei nicht diskret gemessenen
Variablen.
Jitterplots sind insbesondere hilfreich, wenn (a) diskrete
Variablen abgebildet werden (z.B. Likert-Skalen), die keine generische
nuancierte Streuung aufweisen und (b) mittelgrosse Stichproben vorliegen
(bei n>10.000 z.B. hilft mesit auch kein Jitter mehr)
Jitterplots halten das Repräsentationsniveau des einfachen
Streudiagramms (ein Punkt=eine Observation), liefern aber keine
datengetreue Abbildung – besonders problematisch ist dies in den
Randbereichen der Verteilungen und/oder wenn die jitter-Paramter zu hoch
gesetzt werden.
Heatmaps (und auch Bubbleplots) liefern zwar datengetreue
Abbildungen, halten aber nicht das Repräsentationsniveau des einfachen
Streudiagramms (da nun nicht mehr jede Einheit über ein eigenes
grafisches Objekt repräsentiert ist)
Das Erscheinungsbild von Heatmaps im Streudiagramm ist
zuschnittsabhängig (wie wurden die bins gewählt?) und somit
manipulativ einsetzbar
Bubbleplots ergeben nur Sinn bei diskreten Variablen mit einer
überschaubaren Anzahl an Ausprägungen
Heatmaps haben bei sehr schwerpunktlastigen Verteilungen nur eine
begrenzte Aussagekraft