SHP Beispielregression - metrische AV
Marco Giesselmann
24. 2. 2025
Das hier vorgestellte Analyseskript dient als vereinfachtes Muster einer empirischen Ausarbeitung der multiplen Regressionsanalyse auf BA-Niveau am Soziologischen Institut der UZH. Es verdeutlicht zudem unsere Standards für Analyse und Ergebnisdarstellung. Gewähr für die Funktionalität des Codes und Korrektheit der Ergebnisse wird nicht übernommen. Fehlermeldungen und Verbesserungsvorschläge bitte an den Autor.
Achtung: Die auf dieser Seite dokumentierten Analysen beruhen auf dem im Datenmanagement-Manual erstellten Datensatz mit Daten aus dem Jahr 2022. Der Auswertungstext bezieht sich allerdings an einigen Stellen noch auf eine ältere Datenversion. Im Laufe des Semesters erfolgt eine Aktualisierung
Beispielhaft untersucht wird der Effekt des Haushaltseinkommens auf die Lebenszufriedenheit auf Basis des SHP. Das Haushaltseinkommen dient dabei als Indikator für individuellen Wohlstand und wird dementsprechend als OECD-gewichtetes Haushaltsnetto (auf Monatsbasis) gemessen. Die Messung der Lebenszufriedenheit erfolgt auf einer typischen 11er Likert-Skala. Die Analyse ist querschnittlich ausgerichtet, obgleich Fragestellung & Variationseigenschaften eine längsschnittliche Analyseperspektive eröffnen - auf die das SHP grundsätzlich auch ausgerichtet ist.
Im querschnittlichen Ansatz erfolgt die empirische Effektabsicherung bei Umfragedaten ausschliesslich über die Integration von Kontrollvariablen. Daher werden in der Analyse zusätzlich das Geschlecht, der Erwerbsstatus, Bildung sowie das Alter berücksichtigt. Das Geschlecht wird zudem als Moderator des Einkommenseffektes modelliert, da unser (in diesem Skript nicht weiter erläutertes) theoretisches Erklärungsmodell unterschiedliche Wirkungsmechanismen für Männer und Frauen etabliert hat. Neben dem bivariaten und dem bereinigten Regressionsmodell wird daher ein Moderationsmodell spezifiziert. Zudem sei angenommen, dass im Rahmen der theoretischen Auseinandersetzung die Wohnungsqualität als wichtige einkommensgebunden Ursache für subjektives Wohlbefinden identifiziert wurde; daher sollen die statistischen Mediationseigenschaften dieser Variable in einem Mediationsmodell empirisch erschlossen werden.
Der vorgelagerte Prozess des Datenmanagements ist nicht in diesem Skript dokumentiert, sondern auf der Seite zum Datenmanagement. Infos zum SHP gibt es auf der Homepage von FORS.
Los geht’s wie immer mit dem Kopf der Syntax:
# BAa
# SHP Analyse zur Lebenszufriedenheit
# Datum: 23.03.2025
# AutorIn: XXXAls nächstes lesen wir die zuvor produzierte Datenmatrix ein und installieren/aktivieren die für die Analyse relevanten Packages.
# Daten einlesen (z.B. von "c:\meine_BA")
library(haven)
datensatz <- read_dta("mein_laufwerk/mein_zielverzeichnis/shp_base2.rds")# install.packages("package")
library(tidyverse)
library(ggplot2)
library(visreg)
library(summarytools)
library(stargazer)
library(fastDummies)
library(labelled)
library(ggridges)
library(Hmisc)
1 Vorbereitungen und Inspektion
Bevor es losgeht verschaffen wir uns einen Überblick über den Datensatz und die Variablen:
- Sind alle wichtigen Variablen enthalten?
- Sie die Variablenklassen (numeric, factor…) stimmig zugewiesen?
- Ist der Datensatz beschränkt auf die angestrebte Stichprobe?
- Sind die Ausprägungen (Min, Max, Mittelwerte, Anzahl Missings)
plausibel?
- Sieht die Datenmatrix ok aus?
dim (shp_base2)## [1] 11438 28tibble::view(shp_base2)
summary(shp_base2)## pid w11101_2022 alter educyears
## Min. :5.101e+03 Min. : 145.4 Min. : 18.00 Min. : 0.00
## 1st Qu.:1.199e+07 1st Qu.: 309.7 1st Qu.: 39.00 1st Qu.:12.00
## Median :4.193e+07 Median : 472.1 Median : 55.00 Median :13.00
## Mean :3.496e+07 Mean : 658.9 Mean : 53.11 Mean :14.47
## 3rd Qu.:4.655e+07 3rd Qu.: 758.4 3rd Qu.: 67.00 3rd Qu.:19.00
## Max. :1.605e+09 Max. :3899.5 Max. :100.00 Max. :21.00
## NA's :824 NA's :59
## geschlecht zivilstand hhgr numkids
## Min. :1.000 Min. :1.000 Min. : 1.000 Min. :0.0000
## 1st Qu.:1.000 1st Qu.:1.000 1st Qu.: 2.000 1st Qu.:0.0000
## Median :2.000 Median :1.000 Median : 2.000 Median :0.0000
## Mean :1.525 Mean :1.519 Mean : 2.607 Mean :0.4128
## 3rd Qu.:2.000 3rd Qu.:2.000 3rd Qu.: 4.000 3rd Qu.:0.0000
## Max. :2.000 Max. :5.000 Max. :10.000 Max. :5.0000
## NA's :1 NA's :7
## erwerb hhnetto idhous22 height
## Min. :1.000 Min. : 453.3 Min. : 51 Min. :1.18
## 1st Qu.:1.000 1st Qu.: 60471.8 1st Qu.: 120011 1st Qu.:1.64
## Median :2.000 Median : 94022.4 Median : 419396 Median :1.70
## Mean :1.981 Mean : 106792.3 Mean : 357779 Mean :1.71
## 3rd Qu.:3.000 3rd Qu.: 135266.8 3rd Qu.: 465691 3rd Qu.:1.78
## Max. :3.000 Max. :1411112.9 Max. :16374512 Max. :2.06
## NA's :47 NA's :16 NA's :431
## weight lifesat health kanton
## Min. : 35.00 Min. : 0.000 Min. :1.000 Min. : 1.00
## 1st Qu.: 62.00 1st Qu.: 7.000 1st Qu.:2.000 1st Qu.: 6.00
## Median : 72.00 Median : 8.000 Median :2.000 Median :16.00
## Mean : 73.45 Mean : 8.003 Mean :2.019 Mean :14.77
## 3rd Qu.: 82.00 3rd Qu.: 9.000 3rd Qu.:2.000 3rd Qu.:23.00
## Max. :190.00 Max. :10.000 Max. :5.000 Max. :26.00
## NA's :777 NA's :501 NA's :44
## zustand anz_zimmer noise sample status_2022
## Min. :1.000 Min. : 1.000 Min. :1.000 Min. :1 Min. :0.00000
## 1st Qu.:2.000 1st Qu.: 3.000 1st Qu.:2.000 1st Qu.:1 1st Qu.:0.00000
## Median :2.000 Median : 4.000 Median :2.000 Median :1 Median :0.00000
## Mean :2.158 Mean : 4.493 Mean :1.803 Mean :1 Mean :0.04153
## 3rd Qu.:2.000 3rd Qu.: 5.000 3rd Qu.:2.000 3rd Qu.:1 3rd Qu.:0.00000
## Max. :3.000 Max. :10.000 Max. :2.000 Max. :1 Max. :1.00000
## NA's :59 NA's :525 NA's :57
## idpers erwach oecd_weight oecd_inc_mon
## Min. :5.101e+03 Min. :1.000 Min. :1.000 Min. : 37.78
## 1st Qu.:1.199e+07 1st Qu.:2.000 1st Qu.:1.500 1st Qu.: 3320.45
## Median :4.193e+07 Median :2.000 Median :1.500 Median : 4614.29
## Mean :3.496e+07 Mean :2.194 Mean :1.721 Mean : 5164.81
## 3rd Qu.:4.655e+07 3rd Qu.:2.000 3rd Qu.:2.100 3rd Qu.: 6166.20
## Max. :1.605e+09 Max. :7.000 Max. :4.900 Max. :117592.74
## NA's :16
## bmi overweight zivilstand_class
## Min. :14.27 Min. :0.0000 Length:11438
## 1st Qu.:21.83 1st Qu.:0.0000 Class :character
## Median :24.22 Median :0.0000 Mode :character
## Mean :25.04 Mean :0.1233
## 3rd Qu.:27.22 3rd Qu.:0.0000
## Max. :67.51 Max. :1.0000
## NA's :886 NA's :886Der Datensatz enthält 28 Variablen und 11438 Personen bzw. Beobachtungen. Die Verteilung der Altersvariable und die konstante Ausprägung der von uns angelegten sample-Variable lassen erkennen, dass wir die Stichprobe bereits im Zuge der Datenaufbereitung eingegrenzt haben: Unsere Grundgesamtheit bilden alle erwachsene Personen der Schweiz, Stichprobe und Daten sind dementsprechend begrenzt auf alle Personen, die mindestens 18 Jahre alt sind und die ein gültiges Interview abgeliefert haben. Letzteres erkennen wir auch an der “status_2022”-Variable, die ausschliesslich die Werte 0 (=gültiges Interview) und 1 (=gültiges Proxy-Interview) aufweist. Entspräche an dieser Stelle der Analysedatensatz nicht unserer Konzeption der Stichprobe, wäre im vorhergehenden Schritt der Datenaufbereitung etwas falsch gelaufen.
Fehlende Werte bzw. Antwortverweigerung scheinen ebenfalls korrekt als “NA”-codiert zu sein - jedenfalls enthält keine Variable negative Ausprägungen, die in den Rohversionen der bereitgestellten Datensätze oftmals für solche Item-Missings stehen.
Zur Sicherheit führen wir die entsprechende Fallauswahl noch mal aus (auch wenn sie hier den bestehenden Datensatz 1:1 reproduziert):
shp_sample<-filter(shp_base2, alter>=18 & sample==1)
dim (shp_sample)## [1] 11438 28 In unsere Analyse gehen auch kategoriale
Variablen, bzw. in R-Terminologie: Faktoren, ein. In
der derzeitigen Fassung des Datensatzes sind diese jedoch noch nicht als
solche definiert. Dies erkennen wir an dem Inspektionsoutput oben, in
dem für die kategorialen Variablen keine Häufigkeitsauszählungen,
sondern Mittelwertsstatistiken ausgewiesen sind (zudem könnten wir über
attributes() oder look_for() schnell zu der
entsprechenden Erkenntnis kommen). Damit aber R kategoriale Variablen
auch als solche verarbeitet (und nicht etwa wie metrische Variablen
behandelt), definieren wir sie vorab typkonsistent:
shp_sample$geschlecht<-as_factor(shp_sample$geschlecht)
shp_sample$erwerb<-as_factor(shp_sample$erwerb)
shp_sample$zustand<-as_factor(shp_sample$zustand)Achtung 1: as_factor() generiert gelegentlich neue Missingkategorien jenseits von NA, welche nach der Faktorisierung wieder in NAs zurück kodiert werden müssen. Dieses Problem tritt hier nicht auf.
Achtung 2: as_factor() legt gelegentlich zusätzliche, leere Variablenkategorien an, die auf den Labels der vormaligen und nicht mehr verwendeten Missing-Kategorien beruhen. Dieses Problem tritt hier auf:
table(shp_sample$geschlecht)##
## .S (-3) .M (-2) .C (-1) Male Female
## 0 0 0 5431 6006Dies führt zwar nicht zu analytischen oder statistischen Fehlern, erzeugt aber oft ärgerlichen Überhang in den Darstellungen. Abhilfe schafft droplevels(), ein base-R Kommando welches unbelegte Kategorien einer Faktorvariable entfernt. Alternativ kann auch fct_drop() aus forcats verwendet werden - insb. wenn die Variablenlabels erhalten bleiben sollen, die bei droplevels aus unerfindlichen Gründen eliminiert werden:
shp_sample$geschlecht<-fct_drop(shp_sample$geschlecht)
shp_sample$erwerb<-fct_drop(shp_sample$erwerb)
shp_sample$zustand<-fct_drop(shp_sample$zustand)
table(shp_sample$geschlecht)##
## Male Female
## 5431 6006Alle relevanten kategorialen Variablen sind nun als Faktoren im
Datensatz angelegt, wie sich leicht (z.B über summary())
nachprüfen lässt:
summary(shp_sample)## pid w11101_2022 alter educyears
## Min. :5.101e+03 Min. : 145.4 Min. : 18.00 Min. : 0.00
## 1st Qu.:1.199e+07 1st Qu.: 309.7 1st Qu.: 39.00 1st Qu.:12.00
## Median :4.193e+07 Median : 472.1 Median : 55.00 Median :13.00
## Mean :3.496e+07 Mean : 658.9 Mean : 53.11 Mean :14.47
## 3rd Qu.:4.655e+07 3rd Qu.: 758.4 3rd Qu.: 67.00 3rd Qu.:19.00
## Max. :1.605e+09 Max. :3899.5 Max. :100.00 Max. :21.00
## NA's :824 NA's :59
## geschlecht zivilstand hhgr numkids
## Male :5431 Min. :1.000 Min. : 1.000 Min. :0.0000
## Female:6006 1st Qu.:1.000 1st Qu.: 2.000 1st Qu.:0.0000
## NA's : 1 Median :1.000 Median : 2.000 Median :0.0000
## Mean :1.519 Mean : 2.607 Mean :0.4128
## 3rd Qu.:2.000 3rd Qu.: 4.000 3rd Qu.:0.0000
## Max. :5.000 Max. :10.000 Max. :5.0000
## NA's :7
## erwerb hhnetto idhous22 height
## Full Time :4322 Min. : 453.3 Min. : 51 Min. :1.18
## Part Time :2967 1st Qu.: 60471.8 1st Qu.: 120011 1st Qu.:1.64
## Not Working:4102 Median : 94022.4 Median : 419396 Median :1.70
## NA's : 47 Mean : 106792.3 Mean : 357779 Mean :1.71
## 3rd Qu.: 135266.8 3rd Qu.: 465691 3rd Qu.:1.78
## Max. :1411112.9 Max. :16374512 Max. :2.06
## NA's :16 NA's :431
## weight lifesat health kanton
## Min. : 35.00 Min. : 0.000 Min. :1.000 Min. : 1.00
## 1st Qu.: 62.00 1st Qu.: 7.000 1st Qu.:2.000 1st Qu.: 6.00
## Median : 72.00 Median : 8.000 Median :2.000 Median :16.00
## Mean : 73.45 Mean : 8.003 Mean :2.019 Mean :14.77
## 3rd Qu.: 82.00 3rd Qu.: 9.000 3rd Qu.:2.000 3rd Qu.:23.00
## Max. :190.00 Max. :10.000 Max. :5.000 Max. :26.00
## NA's :777 NA's :501 NA's :44
## zustand anz_zimmer
## in bad condition : 308 Min. : 1.000
## in good condition but not recently renovated:8966 1st Qu.: 3.000
## new or recently renovated :2105 Median : 4.000
## NA's : 59 Mean : 4.493
## 3rd Qu.: 5.000
## Max. :10.000
## NA's :525
## noise sample status_2022 idpers
## Min. :1.000 Min. :1 Min. :0.00000 Min. :5.101e+03
## 1st Qu.:2.000 1st Qu.:1 1st Qu.:0.00000 1st Qu.:1.199e+07
## Median :2.000 Median :1 Median :0.00000 Median :4.193e+07
## Mean :1.803 Mean :1 Mean :0.04153 Mean :3.496e+07
## 3rd Qu.:2.000 3rd Qu.:1 3rd Qu.:0.00000 3rd Qu.:4.655e+07
## Max. :2.000 Max. :1 Max. :1.00000 Max. :1.605e+09
## NA's :57
## erwach oecd_weight oecd_inc_mon bmi
## Min. :1.000 Min. :1.000 Min. : 37.78 Min. :14.27
## 1st Qu.:2.000 1st Qu.:1.500 1st Qu.: 3320.45 1st Qu.:21.83
## Median :2.000 Median :1.500 Median : 4614.29 Median :24.22
## Mean :2.194 Mean :1.721 Mean : 5164.81 Mean :25.04
## 3rd Qu.:2.000 3rd Qu.:2.100 3rd Qu.: 6166.20 3rd Qu.:27.22
## Max. :7.000 Max. :4.900 Max. :117592.74 Max. :67.51
## NA's :16 NA's :886
## overweight zivilstand_class
## Min. :0.0000 Length:11438
## 1st Qu.:0.0000 Class :character
## Median :0.0000 Mode :character
## Mean :0.1233
## 3rd Qu.:0.0000
## Max. :1.0000
## NA's :886Univariate Illustrationen (Histogramme etc.) von UV und AV gehören zwar meist nicht in die Schriftfassung eurer Arbeit, sind aber nützlich für die interne Inspektion und Vergegenwärtigung der zentralen Variablen.
shp_sample_hist<-filter(shp_sample, oecd_inc_mon<20000)
ggplot(shp_sample_hist, aes(x = oecd_inc_mon)) +
geom_histogram(fill="blue") +
xlab("")+ ylab("Anzahl")+
labs(title="Einkommen in der Schweiz 2022",
subtitle="OECD-gewichtetes monatliches Haushaltnetto",
caption="SHP v24, erwachsene Personen, n=11.514")
shp_sample_bar<-filter(shp_sample, !is.na(lifesat))
ggplot(shp_sample_bar, aes(x = lifesat)) +
geom_bar(aes(y = (..count..)/sum(..count..)), fill="blue") +
coord_flip()+
xlab("")+ ylab("Prozent")+
scale_x_continuous(breaks=c(0,1,2,3,4,5,6,7,8,9,10))+
scale_y_continuous(labels=scales::percent,breaks=c(0,0.10,0.20,0.30, 0.40))+
labs(title="Lebenszufriedenheit in der Schweiz 2022",
subtitle='10-ganz und gar zufrieden, 0-überhaupt nicht zufrieden',
caption="SHP v24, erwachsene Personen, n=10.924")## Warning: The dot-dot notation (`..count..`) was deprecated in ggplot2 3.4.0.
## ℹ Please use `after_stat(count)` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.
2 Stichprobenstatistik
Wichtiges Element der empirischen Ausarbeitung und zentraler Bestandteil des Methodeabschnittes ist die Übersichtstabelle zur Stichprobenstatistik. Vorab nehmen wir die Variablenauswahl vor und beschränken den Datensatz auf die analyserelevanten Merkmale. Damit erleichtern wir die Erstellung der Übersichtstabelle und auch die weitere analytische Ausarbeitung:
shp_sample<-select(shp_sample, pid, lifesat, oecd_inc_mon, alter, educyears, geschlecht, erwerb, zustand, w11101_2022)Eine einfache, aber effektive Funktion zur Erstellung einer deskriptiven Übersichtstabelle bietet das Package table1. Praktischerweise verarbeitet dies Faktor-Variablen und weist für diese in der generierten Tabelle automatisch Häufigkeiten (statt Lage- und Streuungsmasse) aus.
Achtung: Achtet vor Anwendung dieses Tabellen-Kommandos unbedingt darauf, dass alle kategorialen Variablen als Faktoren definiert (siehe oben) wurden. Ansonsten würden deren Ausprägungen vom Kommando als numerische Werte interpretiert und entsprechend unsinnige Tabelleneinträge generieren.
library(table1)
table1(~lifesat+oecd_inc_mon+alter+educyears+geschlecht+erwerb+zustand, data=shp_sample)| Overall (N=11438) |
|
|---|---|
| Satisfaction with Life in General | |
| Mean (SD) | 8.00 (1.42) |
| Median [Min, Max] | 8.00 [0, 10.0] |
| Missing | 501 (4.4%) |
| oecd_inc_mon | |
| Mean (SD) | 5160 (3520) |
| Median [Min, Max] | 4610 [37.8, 118000] |
| Missing | 16 (0.1%) |
| Age of Individual | |
| Mean (SD) | 53.1 (18.3) |
| Median [Min, Max] | 55.0 [18.0, 100] |
| Number of Years of Education | |
| Mean (SD) | 14.5 (3.50) |
| Median [Min, Max] | 13.0 [0, 21.0] |
| Missing | 59 (0.5%) |
| Gender of Individual | |
| Male | 5431 (47.5%) |
| Female | 6006 (52.5%) |
| Missing | 1 (0.0%) |
| Employment Level of Individual | |
| Full Time | 4322 (37.8%) |
| Part Time | 2967 (25.9%) |
| Not Working | 4102 (35.9%) |
| Missing | 47 (0.4%) |
| Condition of current accommodation | |
| in bad condition | 308 (2.7%) |
| in good condition but not recently renovated | 8966 (78.4%) |
| new or recently renovated | 2105 (18.4%) |
| Missing | 59 (0.5%) |
Es fehlen noch:
- geeignete Überschrift
- Anpassungen der Variablennamen
- Löschen der Zeilen zu Kategorien-Relikten oder leeren Kategorien (nach fct_drop meist nicht mehr notwendig)
…umsetzbar am besten direkt in Word nach copy & paste.
Durch den weiter oben angewendeten fct_drop-Befehl tauchen praktischerweise in der Tabelle nur solche Kategorien auf, die auch tatsächlich besetzt sind.
Unkonventionell am Output von table1 ist die zeilenübergreifende Organisation der statistischen Kennwerte, welche in der traditionellen Stichprobenstatistik die Spalten der Übersichtstabelle definieren. Insbesondere bei Analysen mit vielen Variablen bricht table1 daher mit dem Leitbild darstellungsökonomischer Sparsamkeit und Übersichtlichkeit.
Alternative Darstellungen bieten dann die Packages summarytools und stargazer, deren Befehle zur Übersichtsstatistik allerdings keine Faktor-Variablen verarbeiten. Diese müssen folglich zunächst in Sets numerischer Dummy-Variablen rekodiert werden, sofern ihr summarytools und stargazer zur Produktion der Übersichtsstatistik nutzen wollt:
shp_sample_D<-dummy_cols(shp_sample, select_columns=c("geschlecht", "erwerb", "zustand"), ignore_na = TRUE)…so werden im (neu gebildeten) Datensatz neben den grundlegenden
Faktorvariablen auch die davon abgeleiteten Dummies angelegt - und zwar
formal als metrische Variablen (check:
is.numeric(shp_sample_D$geschlecht_Male)). Durch die etwas
mühsame doppelte Variablenredefinition (metrisch→faktor→dummy) werden
kategoriale Variablen nun auch von den Übersichtskommandos in
summarytools und stargazer aufgegriffen.
stats<-summarytools::descr(shp_sample_D, stats = c("N.Valid", "Pct.Valid", "mean", "sd", "min", "max"), transpose=T)
print(stats, method="browser", file="stats.htm")
statsdf<-data.frame(stats)
statsDirekt veröffentlichungswürdig ist der Output so zwar noch nicht, aber der Weg dahin ist nun relativ kurz: der print-Befehl legt eine html-Tabelle im aktuellen Working Directory an, die leicht z.B. nach Word kopiert & dort weiterbearbeitet werden kann. Durch:
- Anpassung der Überschrift
- Löschen der Zeilen zu Kategorien-Relikten oder leeren Kategorien (nach fct_drop meist nicht mehr notwendig)
- Anpassung der Variablen- und Spaltennamen
- Entfernung der Standardabweichung bei kategorialen Variablen
…entsteht binnen 5 Minuten eine nahezu veröffentlichungswürdige Tabelle zur Stichprobenstatistik:

Alternativ hätten wir die oben angelegte descr-Output-Matrix stats_df direkt in Word oder Excel weiterverarbeiten können.
Das Package stargazer kann ebenfalls ein gut übertragbares html-Dokument zur Stichprobenstatistik kreieren. Es bietet insbesondere dann eine gute Alternative, wenn summarytools sich nicht sauber installieren lässt oder Konflikte mit der verwendeten R-Version und dem Betriebssystem erzeugt, was leider häufig berichtet wird.
stargazer(as.data.frame(shp_sample_D), type="text", out="table1.html",
title="Übersichtstabelle: Univariate Statistik", digits=2)Allerdings müssen hier im Rahmen der Nachbearbeitung zusätzlich zu den oben aufgeführten Formatierungsschritten noch die Anteile der NAs per Hand berechnet und ergänzt werden. Bei stargazer-produzierten Tabellen gibt es verschiedene Möglichkeiten des Transfers zur weiteren Bearbeitung. Eine davon: spezifiziere die Tabelle als html-Dokument, öffne dieses im Browser, kopiere sie von dort nach Word und übernehme da die Finalisierung.
Achtung Stichprobenfresser!
Die Übersicht zur Stichprobenstatistik, die typischerweise vor der Reduktion des Datensatzes auf die Modellstichprobe erstellt wird, ist zuvorderst ein wichtiges Instrument der Datenkommunikation, dient aber auch der inneren Vergegenwärtigung möglicher Probleme der Variablenauswahl. Merke: Die besetzungsschwächste Drittvariable prägt die Grösse der Modellstichprobe; daher muss die Kontrollleistung einer Variable immer gegenüber den mit ihrer Integration verbundenen Stichprobeneinbussen abgewogen werden. Die vorliegende Stichprobenstatistik weisst die Lebenszufriedenheit als ausfallsensibelste Variable im Analysedatensatz aus: da dies eine der beiden zentralen Variablen der Analyse ist, sind die entsprechenden Ausfälle hier alternativlos, zudem aber auch nicht besonders gross.
In vielen anderen denkbaren Szenarios könntet ihr aber auf Grundlage eines Nebendarstellers einen Grossteil der Stichprobe verlieren, was in vielen Fällen inakzeptabel wäre. Ihr würdet dann stattdessen entweder (a) auf die Kontrolle des entsprechenden Stichprobenfressers verzichten, (b) eine andere Variable, die ein ähnliches Konzept abbildet, verwenden, oder (c) eine modellierbare Zusatzkategorie “Fehlend” zu den Ausprägungen des Stichprobenfressers integrieren, in welche die nicht-modellierbaren Missings verschoben werden.
2b DAG
Ein Kausaldiagramm bietet, neben der gleichungsbasierten Modelldarstellung, typischerweise eine praktische Möglichkeit, die Entscheidung zur Integration von Drittvariablen (und somit die zentralen Modellannahmen) fundiert und strukturiert zu kommunizieren. Der Code unten beschreibt einen Möglichen Ansatz, ein Kausaldiagramm mit R umsetzen, hat aber mehere Probleme und erzeugt ein DAG weit jenseits jeglicher Publizierbarkeit.
library (dagitty)
library (ggdag)##
## Attache Paket: 'ggdag'## Die folgenden Objekte sind maskiert von 'package:table1':
##
## label, label<-## Die folgenden Objekte sind maskiert von 'package:Hmisc':
##
## label, label<-## Die folgenden Objekte sind maskiert von 'package:summarytools':
##
## label, label<-## Das folgende Objekt ist maskiert 'package:stats':
##
## filterdag<-dagitty('dag{"Einkommen" -> "Lebenszufriedenheit" "Alter" -> "Lebenszufriedenheit" "Einkommen" -> "Wohnungsqualität" "Wohnungsqualität" -> "Lebenszufriedenheit"}')
ggdag(dag) +
theme_void()
3 Bivariate Inspektion und Visualisierung
3.1 Metrische UV
Die deskriptive Aufarbeitung des bivariaten Zusammenhangs von UV und AV dient in erster Linie der Datenexploration. Gleichwohl wertet eine gelungene Visualisierung des bivariaten Zusammenhangs jede Forschungsarbeit auf. Das grundlegende bivariate Visualisierungsinstrument ist das einfache Streudiagramm:
scatterplot <- ggplot(shp_sample,
aes(x = oecd_inc_mon, y = lifesat)) +
geom_point() +
geom_smooth(method=lm, se=F) +
scale_x_continuous(breaks = seq(0,20000,2000)) +
scale_y_continuous(breaks = seq(0,10,1)) +
coord_cartesian(xlim=c(0,20000))+
labs(x = "Monatliches Haushaltsnetto",
y = "Lebenszufriedenheit",
title = "Einkommen und Lebenszufriedenheit in der Schweiz",
caption = "Quelle: SHP v.19, n = 10.924 \nKodierung: 0-überhaupt nicht zufrieden; 10-ganz und gar zufrieden") +
theme_classic()
scatterplot## `geom_smooth()` using formula = 'y ~ x'## Warning: Removed 514 rows containing non-finite outside the scale range
## (`stat_smooth()`).## Warning: Removed 514 rows containing missing values or values outside the scale range
## (`geom_point()`).
Das für grosse Datensätze typische Problem Overplotting ist in dieser Anwendung noch durch den diskreten Charakter der abhängigen Variable und die starke Belegung der Modalkategorie (~40% bei Lebenszufriedenheit=8) verschärft. R bietet verschiedene Variationen des einfachen Scatterplots, die solche Probleme in verschiedenen Anwendungssituationen jeweils graduell abfedern können.
Empfehlung: In der konkreten empirischen Situation immer nur eine der Varianten - nämlich die, die den Charakter des Zusammenhangs am besten abzubilden vermag - in den Bericht (bzw. die Präsentation oder das Poster) integrieren.
Der Jitterplot fügt den Werten eine zufällige Streuungskomponente zu, zudem lässt das alpha-Argument die Punkte transparent erscheinen, so dass Überlagerungen besser sichtbar werden. Wichtig: Die Spezifikation des geom_jitter-Befehls sollte bei quasi-metrischen Variablen den diskreten Charakter der Variablen nicht aufheben - indem, wie hier, kleine Lücken zwischen den horizontalen Streusäulen belassen werden. Manchmal muss dafür das “jitter”-Argument zwar noch weitergehend als hier spezifiziert werden, oftmals funktioniert aber der Default gut im Sinne dieses Leitbilds.
scatterplot <- ggplot(shp_sample,
aes(x = oecd_inc_mon, y = lifesat)) +
geom_jitter(size=2, alpha=0.1) +
geom_smooth(method=lm, se=F) +
scale_x_continuous(breaks = seq(0,18000,2000)) +
scale_y_continuous(breaks = seq(0,10,1)) +
coord_cartesian(xlim=c(0,18000))+
labs(x = "Monatliches Haushaltsnetto",
y = "Lebenszufriedenheit",
title = "Einkommen und Lebenszufriedenheit in der Schweiz",
caption = "Quelle: SHP v.19, n = 10.924 \nKodierung: 0-überhaupt nicht zufrieden; 10-ganz und gar zufrieden") +
theme_classic()
scatterplot## `geom_smooth()` using formula = 'y ~ x'
Die Heatmap vermag in diesem Beispiel ebenfalls den Charakter des Zusammenhangs zu visualisieren. Dieses Visualisierungsinstrument ist insbesondere dann hilfreich, wenn wir es mit grossen Datensätzen zu tun haben. Andererseits ist ein zurückhaltender Einsatz dieser Darstellungsoption im Rahmen der Zusammenhangsanalyse geboten, da zum einen das zentrale Repräsentationsniveau (1 Messung = 1 Darstellungspunkt) aufgegeben wird und zum anderen die implizite Klassierung Zusammenhänge verschleiern oder überbetonen kann.
Wichtig: Kalibriere über das bins-Argument die Geographie bzw. Klassenbildung der Map so, dass keine strukturbedingten Lücken in der Abbildung entstehen. Nur dann können abgebildete Lücken eindeutig, nämlich als geringe bzw. fehlende Belegung, interpretiert werden.
heatmap <- ggplot(shp_sample,
aes(x = oecd_inc_mon, y = lifesat)) +
geom_bin2d(bins = c(40, 10)) +
geom_smooth(method=lm, se=F) +
scale_x_continuous(breaks = seq(0,20000,2000)) +
scale_y_continuous(breaks = seq(0,10,1)) +
coord_cartesian(xlim=c(0,14000))+
scale_fill_gradient(low = "azure", high="darkblue", name = "Anzahl") +
labs(x = "Monatliches Haushaltsnetto",
y = "Lebenszufriedenheit",
title = "Einkommen und Lebenszufriedenheit in der Schweiz",
caption = "Quelle: SHP v.19, n = 10.924 \nKodierung: 0-überhaupt nicht zufrieden; 10-ganz und gar zufrieden") +
theme_classic()
heatmap## `geom_smooth()` using formula = 'y ~ x'
Der multiple Boxplot ist häufig hilfreich zur Visualisierung der Schwerpunktverschiebung - hier allerdings nicht, weil sich Median und Quartile der Lebenszufriedenheit über die Einkommensverteilung kaum verschieben. Veränderungen der Lebenszufriedenheit mit zunehmenden Einkommen zeigen sich subtiler, unterhalb der Sensititvät relativ grober Lagemasse, weshalb auf sie abstellende Illustrationen in dieser empirischen Anwendung kein geeignetes Visualisierungsinstrument sind:
ggplot(shp_sample, aes(x=oecd_inc_mon, y=lifesat)) +
scale_y_continuous(breaks = seq(0,10,1)) +
coord_cartesian(xlim=c(0,14000))+
geom_boxplot(aes(group = cut_width(oecd_inc_mon, 1000)), orientation = "oecd_inc_mon", outlier.alpha = 0.1)+
labs(x = "Monatliches Haushaltsnetto (in 1000er-Klassen)",
y = "Lebenszufriedenheit",
title = "Einkommen und Lebenszufriedenheit in der Schweiz",
caption = "Quelle: SHP v.19, n = 10.924 \nKodierung: 0-überhaupt nicht zufrieden; 10-ganz und gar zufrieden") +
theme_classic()
Etwas besser funktioniert das differenzierte bzw. konditionale Stapeldiagramm. Eigentlich ordinalen Variablen vorbehalten, mag es in bestimmten Variablen- und Datenkonstellationen ein geeignetes Mittel zur Visualisierung des Zusammenhangs zweier (quasi-)metrischer Variablen sein:
# Klassifizierung der UV "Einkommen"
shp_sample$oecd_inc_mon_category <- cut(
shp_sample$oecd_inc_mon,
breaks = c(-Inf, 2500, 5000, 7500, Inf),
labels = c("0-2500", "2501-5000","5001-7500", "7501+"),
right = TRUE
)
# Klassifizierungscheck
table(shp_sample$oecd_inc_mon_category)##
## 0-2500 2501-5000 5001-7500 7501+
## 1478 5058 3376 1510# Eliminiere NA beider Variablen (werden sonst im Stapeldiagramm dargestellt)
shp_sample_clean <- shp_sample[!is.na(shp_sample$lifesat) & !is.na(shp_sample$oecd_inc_mon_category), ]
# Ordne die Kategorien der Lebenszufriedenheit so, dass niedrige Werte unten gestapelt werden
shp_sample_clean$lifesat <- factor(shp_sample_clean$lifesat, levels = rev(levels(factor(shp_sample$lifesat))))
# Erstelle die nach Bildungsklassen differenzierten Stapeldiagramme der Lebenszufriedenheit
a<-ggplot(shp_sample_clean, aes(x = oecd_inc_mon_category, fill = lifesat)) +
geom_bar(position = "fill") +
labs(
x = "Haushaltseinkommen (Klassiert)",
y = "Prozent",
fill = "Lebenszufriedennheit",
title = "Stapeldiagramm: Lebenszufriedenheit nach Bildungsjahren"
) +
scale_y_continuous(labels = scales::percent_format()) + scale_fill_brewer(palette = "Set3")+
theme_minimal()
a
Es zeigt hier an, dass Lebenzufriedenheiten <7 in höheren Einkommenklassen deutlich seltener als in niedrigen berichtet werden, was mit einer stärkeren Verbreitung insbesondere mittelhoher Lebenszufriedenheiten (Kategorien 8 und 9) in höheren Einkommsnkategorien einhergeht. Diese Darstellungsform kann immer dann den typischen metrischen Visualisierungsinstrumenten vorgezogen werden, wenn die Ausprägungen der metrischen Variablen nicht nur als Elemente einer Skala, sondern zugleich als aussagekräftige Kategorien gedeutet werden können. Diese Bedingung ist im vorliegenden Praxisbeispiel leidlich gegeben - Die Klassierung von Einkommen anhand verteilungsbasierter Parameter ist nicht unüblich und die Lebenszufriedenheit wartet mit einer begrenzten Anzahl diskreter Ausprägungen auf - trotzdem würde man wahrscheinlich in diesem empirischen Fall die genuin metrischen, ans Streudiagramm angelehnte Darstellungsformen vorziehen: Schlicht, weil sie enger an der Logik der Regressionsanalyse angelegt sind und dem Niveau der beteiligten Variablen Tribut zollen.
Insbesondere zur Linearitätsdiagnose geeignet ist der Binplot bzw. binned Scatterplot. Hier repräsentieren die Punkte keine Beobachtungen, sondern Mittelwerte der AV in Kategorien bzw. Klassen der UV. Die horizontalen Abstände informieren zudem über die jeweilige Dichte der Verteilung der UV. Diese Darstellung hilft oft bei der visuellen Einschätzung der Zusammenhangsform im Rahmen der Linearitätsdiagnose. Eine zentrale bivariate Information, nämlich die konditionale Streuung der abhängigen Variablen, wird im Binplot allerdings nicht abgebildet, weshalb sein Nutzen zur Zusammenhangsdeskription insgesamt begrenzt ist:
library(binsreg)
shp_sample_bins<-as.data.frame(shp_sample)
# Convert variables to numeric
shp_sample_bins$oecd_num <- as.numeric(as.character(shp_sample_bins$oecd_inc_mon))
shp_sample_bins$lifesat_num <- as.numeric(as.character(shp_sample_bins$lifesat))
binsreg (data=shp_sample_bins, x=oecd_inc_mon, y=lifesat) 
## Call: binsreg
##
## Binscatter Plot
## Bin/Degree selection method (binsmethod) = IMSE direct plug-in (select # of bins)
## Placement (binspos) = Quantile-spaced
## Derivative (deriv) = 0
##
## Group (by) = Full Sample
## Sample size (n) = 10924
## # of distinct values (Ndist) = 7071
## # of clusters (Nclust) = NA
## dots, degree (p) = 0
## dots, smoothness (s) = 0
## # of bins (nbins) = 29binsreg ist nicht besonders objektneutral. Er bedarf also, wie im Befehlsblock oben angedeutet, einer bestimmten Spezifikation bzw. Klassifizierung von Daten und Variablen. Eine weitere Schwäche des binsreg- Befehl sind die beschränkten Möglichkeiten zur graphischen Aufbereitung und Annotation. So gibt es z.B. keine Möglichkeit, Titel etc. hinzuzufügen. Dazu muss relativ aufwendig zunächst ein ggplot-Objekt auf Basis des binsreg-Objektes Kreiert werden:
# Run the binned scatterplot regression analysis and store the output
binsreg_output <- binsreg(data = shp_sample_bins, x = oecd_num, y = lifesat_num)# Create the ggplot object from the binsreg output
bins_plot <- ggplot(data = ggplot_build(binsreg_output$bins_plot)$data[[1]], aes(x = x, y = y)) +
geom_point(size=3) +
ggtitle ("Binned Scatterplot: Lebenszufriedenheit nach Einkommensgruppen") +
ylim(7.5, 8.5) +
labs(y = "Mittlere Lebenszufriedenheit",
x = "Haushaltsnetto (Gruppiert)",
caption = "Quelle: SHP v.19, n = 10.924")
bins_plot
Fazit: Die Abbildungen vermögen alle nicht 100%ig zu überzeugen, was insbesondere den vielen Datenpunkten bzw. der grossen Stichprobe geschuldet ist. Jitterplot, Heatmap, Stapeldiagramm und Binmap funktionieren einigermassen und wären in diesem Fall veröffentlichungswürdig. Alternativ hätten wir mit einer einfachen tabellarischen Darstellung des bivariaten Zusammenhangs arbeiten können, in der wir den Mittelwert der Lebenszufriedenheit zwischen verschiedenen Einkommensklassen vergleichen (siehe Code in Abschnitt 4 weiter unten).
Deutlich wird, dass (a) der Zusammenhang zwischen dem Einkommen und der Lebenszufriedenheit positiv ist und (b) dies insbesondere in der unteren Hälfte der Einkommensskala gilt. Diese Erkenntnis tragen wir mit in den nächsten Abschnitt, der Linearitätsdiagnose. Vorab aber noch ein kurzer Exkurs zur bivariaten Illustration kategorialer unabhängiger Variablen.
3.2 Kategoriale UV
Ist das zentrale unabhängige Merkmal nicht metrisch, sondern kategorial, ist der Boxplot (oder sein engster Verwandter, der Violinplot) das standardmässige bivariate Visualisierungsinstrument. Angenommen, unsere Hypothese würde sich nicht auf die zufriedenheitsstiftende Wirkung des Einkommens, sondern der Wohnsituation beziehen, wäre dies also der naheliegende Visualisierungsansatz:
shp_sample_box<-filter(shp_sample, !is.na(zustand))
ggplot(shp_sample_box, aes(x=zustand, y=lifesat)) +
scale_y_continuous(breaks = seq(0,10,1)) +
geom_boxplot(orientation = "zustand", outlier.alpha = 0.05, outlier.size = 5)+
labs(x = "Zustand der Wohnung",
y = "Lebenszufriedenheit",
title = "Wohnungsqualität und Lebenszufriedenheit in der Schweiz",
caption = "Quelle: SHP v.19, n = 10.924 \nKodierung: 0-überhaupt nicht zufrieden; 10-ganz und gar zufrieden") +
theme_classic()
… hier aber, aufgrund der starken Konzentration der AV, auch nicht besonders überzeugend. Alternativ böte sich auch hier eine Illustration über Punktwolken an, die, umgesetzt als Jitterplot, tatsächlich etwas besser funktioniert:
shp_sample_box<-filter(shp_sample, !is.na(zustand))
gg_box<-ggplot(shp_sample_box, aes(x=zustand, y=lifesat)) +
scale_y_continuous(breaks = seq(0,10,1)) +
scale_x_discrete(labels=c("in bad condition" = "Schlecht" ,"in good condition but not recently renovated" = "Gut, aber unrenoviert",
"new or recently renovated" = "Gut, renoviert oder neu"))+
labs(x = "Zustand der Wohnung",
y = "Lebenszufriedenheit",
title = "Wohnungsqualität und Lebenszufriedenheit in der Schweiz",
caption = "Quelle: SHP v.19, n = 10.924 \nKodierung: 0-überhaupt nicht zufrieden; 10-ganz und gar zufrieden") +
theme_classic()+
geom_jitter(alpha=0.1)
gg_box
Diese Darstellungsform (Jitterplot mit kategorialer UV) wird oft auch Stripplot genannt. Dass sie gelegentlich auch bei grossen Datensätzen zu sinnvollen Visualisierungen führen kann, bezeugt folgendes Beispiel: Hier wird zu Demonstrationszwecken der bivariate Zusammenhang zwischen dem Geschlecht und dem BMI dargestellt. Die Funktionalitäten von Jitter- und Boxplot werden dabei kombiniert, ausserdem der Bildausschnitt über coord_cartesian konzentriert und beide geom-Funktionen so spezifiziert, dass eine gute Darstellung herauskommt:
shp_sample_box2<-filter(shp_base2, !is.na(geschlecht))
shp_sample_box2$geschlecht<-as_factor(shp_sample_box2$geschlecht)
gg_box2 <- ggplot(shp_sample_box2, aes(x = geschlecht, y = bmi, fill = geschlecht)) +
scale_y_continuous(breaks = seq(10, 40, 5)) +
coord_cartesian(ylim = c(13, 45)) +
labs(x = "Geschlecht",
y = "BMI",
title = "Mittelwertvergleich: Geschlecht und BMI",
caption = "Quelle: SHP v.19, n = 10.924") +
theme_classic() +
geom_boxplot(outlier.shape = NA) +
geom_jitter(alpha = 0.08, position = position_jitter(0.33)) +
guides(fill = FALSE) +
scale_x_discrete(labels = c("Männer", "Frauen"))
gg_box2
In Fällen, in denen keine der vorgeschlagenen Visualisierungen eine inhaltlich aussagekräftige Darstellung erzeugt, kann die obligatorische bivariate Statistik auch einfach über einen tabellarisch aufbereiteten Mittelwertvergleich erfolgen:
shp_sample_gr<-group_by(shp_base2, geschlecht)
summarise_at(shp_sample_gr, vars(bmi), list(bmi=mean), na.rm=T)## # A tibble: 3 × 2
## geschlecht bmi
## <dbl+lbl> <dbl>
## 1 1 [Male] 26.0
## 2 2 [Female] 24.2
## 3 NA 22.7
3.3 Weiterverarbeitung von Grafiken
Der einfachste Weg, die R-Grafik in Euren Report zu bekommen, ist die Export-Funktion unter Plots rechts unten in der Konsole: Klicke zunächst auf Export direkt über dem Plot, wähle dann Format und Speicherort. Zur Weiterverarbeitung in Word oder PowerPoint speichert ihr den Plot am besten als Image.
Etwas eleganter ist der Code-integrierte Export; hier könnt ihr das erstellte Image jederzeit frisch und ohne viel Aufwand mit den einmal gewählten Einstellungen reproduzieren:
jpeg("scatterbox.jpeg", width=620, height=480, quality=100)
gg_box2
dev.off()Noch praktischer ist die ggplot-integrierte Exportoption ggsave(), die bei ggplot-erstellten Grafikobjekten zuverlässig anwendbar ist.
gg_box2
ggsave(filename = "scatterbox.png") # der Default funktioniert meist dann ok, wenn keine Grössenspezifikationen im Rahmen des ggplot-Befehlt vorgenommen wurden.
ggsave(filename = "scatterbox2.png", width = 11, height = 11, dpi=500, units = "cm") # ...andernfalls müssen im Rahmen des Befehls entsprechende Anpassungen, typischerweise durch trial & error, vorgenommen werden.
ggsave(filename = "scatterbox.pdf", width = 11, height = 11, dpi=500, units = "cm") # ...für Poster aber auch grundsätzlich praktisch: Grafiken als (pixelunabhängige) .pdf speichern.
4 Linearitätsdiagnose
Die Linearität bzw. die Form des Zusammenhangs sollte vor jeder Regressionsanalyse mit metrischer unabhängiger Variable theoretisch begründet und empirisch abgestützt werden. Obgleich nicht jede Linearitätsabweichung direkt zu einer Variablentransformation führen muss, können so die Analyseergebnisse später besser eingeordnet werden. Wie meistens bei Einkommensdeterminanten können wir hier eine Sättigung des Effektes bei hohen Werten theoretisch gut begründen. Die Diagramme oben, insbesondere der Binsplot, stützen solche Vermutungen. Sowohl die Multigruppenanalyse als auch der klassenspezifische Mittelwertvergleich können zur explorativ-empirischen Fundierung dieser Vermutung eingesetzt werden.
Die Multigruppenanalyse vergleicht die Steigungskoeffizienten zwischen verschiedenen Abschnitten der UV:
shp_sample_g1<-filter(shp_sample, oecd_inc_mon<4300)
shp_sample_g2<-filter(shp_sample, oecd_inc_mon>=4300)
lm(lifesat~oecd_inc_mon, shp_sample_g1)##
## Call:
## lm(formula = lifesat ~ oecd_inc_mon, data = shp_sample_g1)
##
## Coefficients:
## (Intercept) oecd_inc_mon
## 7.4232520 0.0001463lm(lifesat~oecd_inc_mon, shp_sample_g2)##
## Call:
## lm(formula = lifesat ~ oecd_inc_mon, data = shp_sample_g2)
##
## Coefficients:
## (Intercept) oecd_inc_mon
## 7.991e+00 1.788e-05Die getrennt nach Einkommensbereich durchgeführten Zusammenhangsanalysen zeigen einen deutlich abflachenden Einkommenseffekt: Einkommenszuwächse führen in der unteren Hälfte der Einkommensverteilung zu einer deutlich stärkeren Zunahme der Lebenszufriedenheit als in der oberen. Dies wird auch deutlich, wenn wir ein alternatives Instrument der Linearitätsdiagnose einsetzen, den kategorien- bzw. klassenspezifischen Mittelwertvergleich. Hierzu klassieren wir zunächst die Einkommensvariable in Intervalle mit konstanter Breite:
shp_sample$incgroup<-cut(shp_sample$oecd_inc_mon, breaks=c(0, 2500, 5000, 7500, 10000, 12500, Inf), labels=c("0/2.5k","2.5/5k","5/7.5k","7.5/10k","10/12.5k", "12.5k+"), include.lowest=TRUE)Anschliessend lassen wir die klassenspezifischen Mittelwerte der abhängigen Variable berechnen:
shp_sample_gr<-group_by(shp_sample, incgroup)
summarise_at(shp_sample_gr, vars(lifesat), list(Lifesat=mean), na.rm=T)## # A tibble: 7 × 2
## incgroup Lifesat
## <fct> <dbl>
## 1 0/2.5k 7.69
## 2 2.5/5k 7.95
## 3 5/7.5k 8.09
## 4 7.5/10k 8.26
## 5 10/12.5k 8.31
## 6 12.5k+ 8.35
## 7 <NA> 7.38Auch anhand des Mittelwertvergleichs der Lebenszufriedenheit zwischen den Einkommensklassen erkennen wir einen deutlich abflachenden Einfluss: Der mit einem Einkommensgruppensprung verbundene Gewinn an Lebenszufriedenheit ist im unteren Bereich der Einkommensgruppenverteilung grösser als im oberen (die Logik des so durchgeführten klassenspezifischen Mittelwertsvergleichs ist übrigens dieselbe, die auch der oben eingeführten Binsplot realisiert). Unsere Vorüberlegung zur nicht-linearen Zusammenhangsform wird also empirisch gestützt: Es erscheint theoretisch geboten und empirisch folgerichtig, die unabhängigen Variable in der Analyse zu logarithmieren. Diese Transformation führt zur Begradigung des Zusammenhangs, greift also den gedrosselten Einkommenseffekt auf (und erhält gleichzeitig die, wenn nun auch veränderte, Interpretationsfähigkeit des Koeffizienten).
Empfehlung zur Einbindung der Linearitätsdiagnose: Biete die theoretisch gestützte Begründung zur Zusammenhangsform (linear vs. logarithmisch vs. quadratisch) im Rahmen des Methodenteils der Arbeit an; Verweise dabei auf die empirische Absicherung bzw. Multigruppenanalyse oder klassenspezifische Analyse, die du im Anhang der Arbeit dokumentierst. Achtung: Problematisierungen der Zusammenhangsform und korrigierende Re-Linearisierungen sind nur relevant bei einer metrischen Spezifikation der UV, wenn also ein alle Ausprägungen übergreifender Zusammenhang per Regressionsgerade die gesamte Skala der UV überspannt. Wenn aber die unabhängige Variable nicht metrisch ist (oder zwar metrisch ist, aber über klassierte Kategorien gemessen und integriert wird), werden automatisch ganz unterschiedliche Zusammenhangsmuster zugelassen und in der Analyse abgebildet. Die Problematisierung der Zusammenhangsform ist dann hinfällig, bzw.: Nicht-Linearität wird dann implizit durch die Klassierung aufgegriffen und abgebildet.
5 Multivariate Regressionsschätzung
5.1 Fallzahlharmonisierung
Bevor wir die multivariate regressionsbasierte Analysereihe etablieren, schränken wir die Stichprobe auf Merkmalsträger mit gültigen Messungen in allen an der Analyse beteiligten Variablen ein, um einer Konvention folgend die Fallzahl über die Modellreihe konstant zu halten.
Achtung: Diesen Schritt bitte erst dann durchführen, wenn alle nicht modellierten Variablen aus dem Datensatz entfernt sind (siehe Abschnitt 2) und Ihr Euch zudem vergewissert habt, dass keine unnötigen “Stichprobenfresser” im Modell sind. Ausserdem darf sich die Einschränkung der Fälle auf komplette Messreihen ausschliesslich auf die multivariate Analyse beziehen. Sowohl in der Stichprobenstatistik als auch den bivariaten Analysen sollte mit der vollständigen Stichprobe bzw. allen zur Verfügung stehenden Fällen gearbeitet werden
shp_model<-drop_na(shp_sample)5.2 Bivariates- und Nettomodell
Los geht’s mit der regressionsbasierten Analyse des einfachen bivariaten Zusammenhangs, quasi als Brücke von der deskriptiven, bivariaten Darstellung in die Modellreihe. Die oben begründete Logarithmierung der UV kann bei Verwendung des für Regressionsanalysen einschlägigen lm-Kommandos praktischerweise direkt im Rahmen des Befehls erfolgen:
bivariat<-lm(lifesat~log(oecd_inc_mon), shp_model)
summary (bivariat)##
## Call:
## lm(formula = lifesat ~ log(oecd_inc_mon), data = shp_model)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.1370 -0.8238 0.0092 0.9485 2.9975
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.42244 0.20778 26.1 <2e-16 ***
## log(oecd_inc_mon) 0.30822 0.02467 12.5 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.404 on 10493 degrees of freedom
## Multiple R-squared: 0.01466, Adjusted R-squared: 0.01457
## F-statistic: 156.2 on 1 and 10493 DF, p-value: < 2.2e-16Ad-hoc Interpretation: Mit jedem Prozent Einkommenszuwachs steigt die Lebenszufriedenheit im Mittel um 0,003 Skalenpunkte. Um also etwa einen drittel Skalenpunkt der Lebenszufriedenheit zuzulegen, muss dein Einkommen 100 mal um 1% (Achtung: Das sind nicht 100%, sondern etwa 170% - Stichwort: Zinseszins), erhöht werden…
Das zentrales Analysemodell, welches die Effektinterpretation anvisiert und somit zur Hypothesenprüfung eingesetzt wird, ist üblicherweise das Nettomodell (manchmal auch bereinigtes Modell, Modell 2 oder, etwas euphemistisch, Kausalmodell genannt), welches den Effekt der als Störmerkmale identifizierten Variablen durch deren Integration abkoppelt. Die Spezifikationsstrategie des Nettomodells sollte im Methodenabschnitt erläutert und begründet werden (z.B. über eine Gleichung oder Pfaddiagram (DAG)). In unserer Beispielanalyse spezifizieren wir folgende Drittvariablen als Störmerkmale:
- Bildung: über die “Bildungsjahre” als metrische Variable
- Alter: viele abhängige Merkmale spannen über dem Alter einen U- oder umgekehrt U-förmigen Verlauf auf. Wir überprüfen das nicht weiter (da es sich beim Alter lediglich um eine Kontrollvariable handelt) sondern nehmen einfach eine entsprechende quadratische Transformation der Altersvariablen vor
- Geschlecht: die binäre Geschlechtervariable spezifizieren wir als Dummy- bzw. Faktor-Variable (macht R automatisch, wenn die Variable entsprechend angelegt ist), deren Koeffizient als Unterschied in der Lebenszufriedenheit zwischen Männern und Frauen gedeutet werden kann
- Erwerbsstatus: Der Erwerbstatus ist als kategoriale
Variable mit 3 Ausprägungen gemessen, wir spezifizieren sie folglich
ebenfalls (automatisch) als Faktor-Variable. Bei mehr als zwei
Ausprägungen wird dabei im Rahmen des lm-Kommandos
automatisch ein Set von Dummy-Variablen in die Analyse integriert, deren
Koeffizienten sich jeweils als durchschnittliche Differenz in der
Lebenszufriedenheit zur Referenzkategorie interpretieren lassen.
Referenzkategorie ist per Default diejenige mit der niedrigsten
Codierung (hier: Full-time)
options(scipen=1, digits=4)
netto<-lm(lifesat~log(oecd_inc_mon)+educyears+poly(alter, 2, raw=TRUE)+geschlecht+erwerb, shp_model)
summary (netto)##
## Call:
## lm(formula = lifesat ~ log(oecd_inc_mon) + educyears + poly(alter,
## 2, raw = TRUE) + geschlecht + erwerb, data = shp_model)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.424 -0.719 0.063 0.954 3.348
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.0293659 0.2366760 21.25 < 2e-16 ***
## log(oecd_inc_mon) 0.3422642 0.0261493 13.09 < 2e-16 ***
## educyears 0.0000962 0.0041922 0.02 0.9817
## poly(alter, 2, raw = TRUE)1 -0.0118884 0.0044255 -2.69 0.0072 **
## poly(alter, 2, raw = TRUE)2 0.0002296 0.0000443 5.18 2.3e-07 ***
## geschlechtFemale 0.0395265 0.0291454 1.36 0.1751
## erwerbPart Time 0.0870344 0.0366832 2.37 0.0177 *
## erwerbNot Working -0.0984871 0.0430154 -2.29 0.0221 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.39 on 10487 degrees of freedom
## Multiple R-squared: 0.0349, Adjusted R-squared: 0.0343
## F-statistic: 54.2 on 7 and 10487 DF, p-value: <2e-16Hinweis: Der erste Befehl im Chunk oben sorgt dafür, dass (die meisten) Zahlenwerte im Output im Dezimalsystem dargestellt werden und so besser lesbar sind.
Ad-hoc Interpretation: Der bereinigte Koeffizient hat sich kaum gegenüber der bivariaten Regressionsschätzung verändert: auch unter Konstanthaltung potentieller Störmerkmale bräuchte es etwa 30 Einkommenssprünge à 1 Prozent, um einen zehntel Skalenpunkt Lebenszufriedenheit zu gewinnen. Inhaltlich betrachtet ist dies zumindest kein grosser Effekt, aus statistischer Perspektive ist der Koeffizient jedoch hochsignifikant. Formal-statistisch kann die Nullhypothese also abgelehnt werden.
5.3 Moderationsmodell
Falls Erklärungsmodell und Hypothese eine Wechselwirkung benennen, spezifizieren wir zusätzlich ein Moderationsmodell. Hier, in unserer Beispielanalyse, integrieren wir einen Interaktionsterm Einkommen * Geschlecht - setzen also voraus, dass im theoretischen Abschnitt nicht nur für einen Einkommenseffekt argumentiert wurde, sondern auch für dessen geschlechtsspezifisch Ausbildung.
moderation<-lm(lifesat~log(oecd_inc_mon)*geschlecht+educyears+poly(alter, 2, raw=TRUE)+erwerb, shp_model)
summary (moderation, digits=max(3))##
## Call:
## lm(formula = lifesat ~ log(oecd_inc_mon) * geschlecht + educyears +
## poly(alter, 2, raw = TRUE) + erwerb, data = shp_model)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.423 -0.719 0.062 0.953 3.381
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.9329310 0.3265716 15.11 < 2e-16 ***
## log(oecd_inc_mon) 0.3536962 0.0373542 9.47 < 2e-16 ***
## geschlechtFemale 0.2171401 0.4154451 0.52 0.6012
## educyears 0.0000884 0.0041924 0.02 0.9832
## poly(alter, 2, raw = TRUE)1 -0.0118735 0.0044258 -2.68 0.0073 **
## poly(alter, 2, raw = TRUE)2 0.0002292 0.0000444 5.17 2.4e-07 ***
## erwerbPart Time 0.0880063 0.0367546 2.39 0.0167 *
## erwerbNot Working -0.0976694 0.0430593 -2.27 0.0233 *
## log(oecd_inc_mon):geschlechtFemale -0.0211482 0.0493446 -0.43 0.6682
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.39 on 10486 degrees of freedom
## Multiple R-squared: 0.0349, Adjusted R-squared: 0.0342
## F-statistic: 47.5 on 8 and 10486 DF, p-value: <2e-16Der Koeffizient des Produktterms misst hier den Einfluss des Moderators auf den Effekt der unabhängigen Variable. Ad-hoc Interpretation: Für Frauen fällt der Anstieg der Lebenszufriedenheit mit einer einprozentigen Erhöhung des Einkommens im Schnitt um 0.0004 Skalenpunkte niedriger aus als für Männer - ist aber immer noch deutlich im positiven Bereich, der Unterschied im Einkommenseffekt zwischen Frauen und Männern zudem nicht signifikant.
Achtung: Wie fast immer bei Spezifikation eines Interaktionsterms mit metrischer unabhängiger Variable kann der Koeffizient des Haupteffektes der Moderatorvariable - hier: Geschlecht - nicht sinnvoll interpretiert werden, da dieser sich, wie sich leicht algebraisch zeigen liesse, nun ausschliesslich auf den Nullpunkt der moderierten Variable - also nulljährige Personen - bezieht.
5.4 Mediationsmodell
Falls Pfade aus dem Erklärungsmodell über Drittvariablen abgebildet werden können, integrieren wir bei vorhandenem Erkenntnisinteresse entsprechende Mediatoren in zusätzlichen Analysen. Damit können wir die indirekten, über die entsprechenden Drittvariablen vermittelten Effekt vom Koeffizienten der UV abspalten und schliesslich die Veränderung zum Netto-Koeffizienten als Indiz für den Mediationsmechanismus - und somit empirische Stütze für die angebotene theoretische Erklärung - werten. Für diese Beispielanalyse nehmen wir an, dass die Wohnqualität als relevanter Effektkanal im Erklärungsmodell eingeführt wurde.
mediation1<-lm(lifesat~log(oecd_inc_mon)+educyears+poly(alter, 2, raw=TRUE)+geschlecht+erwerb+zustand, shp_model)
summary (mediation1)##
## Call:
## lm(formula = lifesat ~ log(oecd_inc_mon) + educyears + poly(alter,
## 2, raw = TRUE) + geschlecht + erwerb + zustand, data = shp_model)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.424 -0.716 0.049 0.945 3.278
##
## Coefficients:
## Estimate Std. Error
## (Intercept) 4.3244032 0.2447358
## log(oecd_inc_mon) 0.3206700 0.0260773
## educyears -0.0009025 0.0041709
## poly(alter, 2, raw = TRUE)1 -0.0117167 0.0044012
## poly(alter, 2, raw = TRUE)2 0.0002269 0.0000441
## geschlechtFemale 0.0354230 0.0289839
## erwerbPart Time 0.0917383 0.0364849
## erwerbNot Working -0.1019978 0.0427747
## zustandin good condition but not recently renovated 0.9079088 0.0870664
## zustandnew or recently renovated 1.0017320 0.0912675
## t value Pr(>|t|)
## (Intercept) 17.67 < 2e-16 ***
## log(oecd_inc_mon) 12.30 < 2e-16 ***
## educyears -0.22 0.8287
## poly(alter, 2, raw = TRUE)1 -2.66 0.0078 **
## poly(alter, 2, raw = TRUE)2 5.15 2.7e-07 ***
## geschlechtFemale 1.22 0.2217
## erwerbPart Time 2.51 0.0119 *
## erwerbNot Working -2.38 0.0171 *
## zustandin good condition but not recently renovated 10.43 < 2e-16 ***
## zustandnew or recently renovated 10.98 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.38 on 10485 degrees of freedom
## Multiple R-squared: 0.0459, Adjusted R-squared: 0.0451
## F-statistic: 56.1 on 9 and 10485 DF, p-value: <2e-16Ad-hoc Interpretation: Der minimale Unterschied im Koeffizienten zwischen Netto- und Mediationsmodell indiziert eine minimale Mediation des Einkommenseffektes über die Wohnsituation. Der Grossteil des Einkommenseffektes wird aber offenbar nicht über die Wohnungsqualität, sondern andere, nicht empirisch spezifizierte Kanäle vermittelt.
5.5 Kategoriale UV
In der hier durchgeführten Analyse laufen die kategorialen Variabelen (Geschlecht, Erwerbszustand, Wohnungszustand) als Kontroll- bzw. Drittmerkmale mit, gelegentlich stehen sie aber auch als zentrale unabhängige Variablen im Fokus des Interesses. Spätestens dann ist es sinnvoll, sich vertieft mit der Frage nach der passenden Referenzkategorie auseinanderzusetzen. Letztlich sollte diese so gewählt werden, dass sich die ausgegebenen Koeffizienten möglichst gut zur direkten Hypothesenbewertung eigenen. Insb. bei ordinalen Variablen (z.B. Bildungsklassen) ergibt es dabei meistens Sinn, eine möglichst prägnante, gut besetzte Kategorie, die sich zudem (bei ordinalen Variablen) am Anfang oder Ende der Skala befindet als Referenzkategorie zu wählen.
Beispielhaft sei die Zuweisung (bzw. Veränderung) der Referenzkategorie anhand der Variable zum Erwerbsstatus demonstriert. Konkret wollen wir erreichen, dass jeweils die Mittelwertunterschiede zur “Nicht Erwerbstätig”-Kategorie in der Regressionstabelle ausgewiesen werden. Zweckmässig ist hierfür der relevel()-Befehl:
shp_model$erwerb <- relevel(shp_model$erwerb , ref = "Not Working")Das Argument ref=() überschreibt dabei die Default-Referenzkategorie mit der hier spezifizierten. Die Mittelwertunterschiede bleiben natürlich identisch, sind im Regressionsoutput jetzt aber anders, entsprechend unserer Referenzsetzung, organisiert:
netto2<-lm(lifesat~log(oecd_inc_mon)+educyears+poly(alter, 2, raw=TRUE)+geschlecht+erwerb, shp_model)
summary(netto2)##
## Call:
## lm(formula = lifesat ~ log(oecd_inc_mon) + educyears + poly(alter,
## 2, raw = TRUE) + geschlecht + erwerb, data = shp_model)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.424 -0.719 0.063 0.954 3.348
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.9308788 0.2260380 21.81 < 2e-16 ***
## log(oecd_inc_mon) 0.3422642 0.0261493 13.09 < 2e-16 ***
## educyears 0.0000962 0.0041922 0.02 0.9817
## poly(alter, 2, raw = TRUE)1 -0.0118884 0.0044255 -2.69 0.0072 **
## poly(alter, 2, raw = TRUE)2 0.0002296 0.0000443 5.18 2.3e-07 ***
## geschlechtFemale 0.0395265 0.0291454 1.36 0.1751
## erwerbFull Time 0.0984871 0.0430154 2.29 0.0221 *
## erwerbPart Time 0.1855216 0.0422182 4.39 1.1e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.39 on 10487 degrees of freedom
## Multiple R-squared: 0.0349, Adjusted R-squared: 0.0343
## F-statistic: 54.2 on 7 and 10487 DF, p-value: <2e-16Die Lebenszufriedenheit Vollzeiterwerbstätiger liegt im Mittel kanpp ein zehntel Skalenpunkt, die Teilzeiterwerbstätiger gar fast ein fünftel Skalenpunkt oberhalb der von Nichterwerbstätigen. Beide Mittelwertunterschiede sind signifikant von 0 verschieden.
Den Mittelwertunterschied der Lebenszufriedenheit zwischen Vollzeit- und Teilzeiterwerbstätigen können wir leicht aus der Tabelle, als Unterschied im Unterschied zur Lebenszufriedenheit der Basiskategorie, ableiten. Wollen wir zustzlich wissen, ob auch dieser Unterschied signifikant von 0 verschieden ist, müssen wir nicht die Regressionsanalyse erneut mit veränderter Referenzkategorie durchführen, sondern können dieses vom R-Kommando emmeans() aus den vorhandenen Modellparametern ableiten lassen:
library(emmeans)## Warning: Paket 'emmeans' wurde unter R Version 4.3.3 erstellt## Welcome to emmeans.
## Caution: You lose important information if you filter this package's results.
## See '? untidy'emm<-emmeans(netto2, ~erwerb)
contrast(emm, method="pairwise", adjust = "none")## contrast estimate SE df t.ratio p.value
## Not Working - Full Time -0.0985 0.0430 10487 -2.290 0.0221
## Not Working - Part Time -0.1855 0.0422 10487 -4.394 <.0001
## Full Time - Part Time -0.0870 0.0367 10487 -2.373 0.0177
##
## Results are averaged over the levels of: geschlechtemmeans() bzw. die Unterfunktion contrast() stellt also sämtliche, aus einem Regressionsfit ableitbare Mittelwertunterschiede zu einer spezifizierten kategorialen Variable dar. Wir erkennen hier, dass der mittlere Lebenszufriedenheitsunterschied zwischen Vollzeit- und Teilzeitarbeitenden ebenfalls statistisch signifikant ist.
6 Tabellarische Darstellung der Regressionsmodelle
Die Regressionstabelle ist obligatorisches Element eines jeden Forschungsbeitrags mit regressionsbasierter Analyse. Insbesondere das Package stargazer erleichtert die Formatierung; ganz ohne manuelles Nachhelfen geht es allerdings nicht.
stargazer(bivariat, netto, moderation, mediation1, type="text",
title="Lineare Regression: Determinanten der Lebenszufriedenheit",
notes=c("in Klammern: Standardfehler",
"SHP v24, n=10.495. Eigene Berechnungen"),
dep.var.labels="", dep.var.caption = "",
column.labels =c("Bivariat", "Netto", "Moderation", "Mediation" ),
order = c(1, 5),
single.row = F,
star.cutoffs = c(.05,.01,.001),
digits=3,
keep.stat=c("n", "rsq"),
digits.extra=5,
out="regtab2.htm")##
## Lineare Regression: Determinanten der Lebenszufriedenheit
## =============================================================================================
##
## Bivariat Netto Moderation Mediation
## (1) (2) (3) (4)
## ---------------------------------------------------------------------------------------------
## log(oecd_inc_mon) 0.308*** 0.342*** 0.354*** 0.321***
## (0.025) (0.026) (0.037) (0.026)
##
## geschlechtFemale 0.040 0.217 0.035
## (0.029) (0.415) (0.029)
##
## educyears 0.0001 0.0001 -0.001
## (0.004) (0.004) (0.004)
##
## poly(alter, 2, raw = TRUE)1 -0.012** -0.012** -0.012**
## (0.004) (0.004) (0.004)
##
## poly(alter, 2, raw = TRUE)2 0.0002*** 0.0002*** 0.0002***
## (0.00004) (0.00004) (0.00004)
##
## erwerbPart Time 0.087* 0.088* 0.092*
## (0.037) (0.037) (0.036)
##
## erwerbNot Working -0.098* -0.098* -0.102*
## (0.043) (0.043) (0.043)
##
## log(oecd_inc_mon):geschlechtFemale -0.021
## (0.049)
##
## zustandin good condition but not recently renovated 0.908***
## (0.087)
##
## zustandnew or recently renovated 1.002***
## (0.091)
##
## Constant 5.422*** 5.029*** 4.933*** 4.324***
## (0.208) (0.237) (0.327) (0.245)
##
## ---------------------------------------------------------------------------------------------
## Observations 10,495 10,495 10,495 10,495
## R2 0.015 0.035 0.035 0.046
## =============================================================================================
## Note: *p<0.05; **p<0.01; ***p<0.001
## in Klammern: Standardfehler
## SHP v24, n=10.495. Eigene BerechnungenAchtung: Vorsicht mit der Befehlsoption covariate labels(). Hiermit lassen sich zwar gut les- und identifizierbare Variablenlabel für den Tabellenoutput vergeben, allerdings muss die Labelliste in der Klammer exakt die Variablenreihenfolge aus dem Regressionsbefehl einhalten. Andernfalls passt die Variablen- bzw. Koeffizientenzuordnung in der Tabelle nicht mehr. Wir empfehlen daher grundsätzlich die Neubeschriftung der Variablen im Rahmen der manuellen Nachbearbeitung statt der automatischen Beschriftung im Befehl. Solltet ihr dennoch mit covariate_labels() arbeiten wollen, vergewissert euch immer, dass die final ausgewiesenen Koeffizienten denen der Rohoutputs entsprechen. In dieser Anwendung lautete der Befehlszusatz:
... covariate.labels=c("Einkommen(ln)", "Weiblich", "Bildungsjahre", "Alter", "Altersq", "Teilzeit", "Nichterwerbstätig", "WeiblichEinkommen", "Akzeptabel", "Exzellent", "Konstante"),stargazer kennt unterschiedliche Ausgabeformate (.txt, .htm,…) die über die Output-Option gesteuert werden können. Unterschiedliche Workflows zum Tabellentransfer sind hier denkbar und unsere Variante ist wahrscheinlich nicht der Goldstandard, aber funktioniert: Ich lasse ein html-Dokument ausgeben, öffne dieses im Browser, kopiere es nach Word und übernehme dort die Finalisierung. Etwa 15 Minuten Arbeitsaufwand hat die Formatierung des Originaloutputs nach diesem Muster zur Produktion folgender Tabelle gekostet Achtung noch nicht an aktuelle Daten angepasst:

Hinweis zu Nachkommastellen: Hier gibt es keine
klaren Standards, wir geben Euch aber folgende Tipps:
- Der Koeffizient der zentralen unabhängigen Variable sollte in
Tabellen und Text mit mindestens 3 substanziellen Zahlen dargestellt
werden (also 151 oder 15.1 oder 0.151, je nach Skalierung). Im Fall oben
bedeutet dies drei Nachkommstellen
- Die Anzahl an Nachkommastellen der anderen Koeffizienten sollte grundsätzlich denen des Hauptkoeffizienten entsprechen, mindestens aber bis zur ersten substanziellen (=ungleich 0) Stelle reichen
- Diese Richtlinien werden nicht immer exakt einzuhalten sein und bedingen häufig zudem die Reskalierung einer (oder mehrerer) Variablen
7 Ausreisserdiagnostik
Der Test deiner Analyseergebnisse auf Robustheit gegenüber Ausreissern ist ein Element der klassischen Regressionsdiagnostik, welches wir für hinreichend relevant halten, um eine Integration in Eure Abschlussarbeit zu empfehlen. Die Ausarbeitung sollte allerdings nicht im Hauptteil, sondern im Anhang der Arbeit dokumentiert werden. Im Hauptteil reicht in der Regel ein kurzer Verweis auf die Robustheit der Ergebnisse gegenüber Ausreisserausschluss; bei fehlender Robustheit sollte dieser Befund dann zusätzlich als Limitation in der Diskussion kritisch diskutiert und eingeordnet werden.
Die Ausreisserbestimmung beruht auf Berechnung des standardisierten Einfluss einzelner Messungen auf den Regressionskoeffizienten, genannt DFbetas. Details zu dieser Strategie könnt ihr z.B. hier nacharbeiten. Zunächst legen wir den Grenzwert fest, ab dem wir eine Messung als “einflussreich” bezeichnen wollen. Wir orientieren uns an dem von Belsley et al. (1980) vorgeschlagene schwellenwert (2/Wurzel(n), hier |0,021|). Anschliessend ermitteln wir, ob es nach dieser Definition einflussreiche Fälle auf den Einkommenskoeffizienten gibt.
summary(dfbetas(netto))## (Intercept) log(oecd_inc_mon) educyears
## Min. :-0.16603 Min. :-0.13983 Min. :-0.09755
## 1st Qu.:-0.00290 1st Qu.:-0.00223 1st Qu.:-0.00348
## Median : 0.00013 Median :-0.00008 Median : 0.00000
## Mean : 0.00000 Mean : 0.00000 Mean : 0.00000
## 3rd Qu.: 0.00234 3rd Qu.: 0.00264 3rd Qu.: 0.00330
## Max. : 0.12619 Max. : 0.21311 Max. : 0.08858
## poly(alter, 2, raw = TRUE)1 poly(alter, 2, raw = TRUE)2 geschlechtFemale
## Min. :-0.09998 Min. :-0.18330 Min. :-0.08347
## 1st Qu.:-0.00289 1st Qu.:-0.00288 1st Qu.:-0.00466
## Median :-0.00001 Median :-0.00001 Median :-0.00014
## Mean : 0.00000 Mean : 0.00000 Mean : 0.00000
## 3rd Qu.: 0.00323 3rd Qu.: 0.00253 3rd Qu.: 0.00441
## Max. : 0.16560 Max. : 0.11636 Max. : 0.08494
## erwerbPart Time erwerbNot Working
## Min. :-0.08880 Min. :-0.14187
## 1st Qu.:-0.00347 1st Qu.:-0.00267
## Median :-0.00009 Median : 0.00001
## Mean : 0.00000 Mean : 0.00000
## 3rd Qu.: 0.00341 3rd Qu.: 0.00308
## Max. : 0.08987 Max. : 0.11600Die Übersichtsstatistik zu den Einflusswerten zeigt, dass es Personen gibt, deren Einfluss auf den Regressionskoeffizienten deutlich oberhalb des Grenzwertes liegt. Wir schliessen diese Personen nun für den Robustheitstest aus der Analyse aus, um zu prüfen, ob das Regressionsergebnis durch diese einflussreichen Fälle unverhältnismässig stark geprägt wird.
dfbetas_matrix <- data.frame(betas=dfbetas(netto))
shp_model_betas <- cbind(shp_model, dfbetas_matrix)
shp_model_oA <- filter(shp_model_betas, betas.log.oecd_inc_mon.<0.021 & betas.log.oecd_inc_mon.>-0.021 )
netto2<-lm(lifesat~log(oecd_inc_mon)+educyears+poly(alter, 2, raw=TRUE)+geschlecht+erwerb, shp_model_oA)
stargazer (netto, netto2, type="text", star.cutoffs = c(.05,.01,.001), column.labels =c("Originalnetto", "ohne Ausreisser"))##
## ==============================================================================
## Dependent variable:
## --------------------------------------------------
## lifesat
## Originalnetto ohne Ausreisser
## (1) (2)
## ------------------------------------------------------------------------------
## log(oecd_inc_mon) 0.342*** 0.340***
## (0.026) (0.027)
##
## educyears 0.0001 -0.003
## (0.004) (0.004)
##
## poly(alter, 2, raw = TRUE)1 -0.012** -0.008*
## (0.004) (0.004)
##
## poly(alter, 2, raw = TRUE)2 0.0002*** 0.0002***
## (0.00004) (0.00004)
##
## geschlechtFemale 0.040 0.004
## (0.029) (0.026)
##
## erwerbFull Time -0.002
## (0.039)
##
## erwerbPart Time 0.087* 0.108**
## (0.037) (0.038)
##
## erwerbNot Working -0.098*
## (0.043)
##
## Constant 5.029*** 5.055***
## (0.237) (0.231)
##
## ------------------------------------------------------------------------------
## Observations 10,495 9,997
## R2 0.035 0.042
## Adjusted R2 0.034 0.041
## Residual Std. Error 1.390 (df = 10487) 1.217 (df = 9989)
## F Statistic 54.210*** (df = 7; 10487) 62.150*** (df = 7; 9989)
## ==============================================================================
## Note: *p<0.05; **p<0.01; ***p<0.001Der zentrale, hypothesenbelastende Koeffizient verändert sich nur minimal. Ergo: Das Originalergebnis ist robust gegenüber einem Ausreisserausschluss nach Belsley et al (1980). Dies sollte nun in einer Fussnote des Ergebnissabschnittes deiner Arbeit berichtet werden. Dass der Geschlechterkoeffizient auf den Ausschluss reagiert ist für uns übrigens nicht relevant, da weder der Hypothesentest noch das Ausschlusskriterium auf diesen Parameter abzielen.
8 Gewichtete Ergebnisse
Das Schweizer Haushaltspanel ist eine grundsätzlich repräsentativ ausgerichtete Studie. Allerdings weichen die rohen Merkmalsverteilungen in den Daten von der Repräsentativität ab; bestimmte Gruppen sind hier über- bzw. unterrepräsentiert. Der Grad an Über- bzw. Unterrepräsentation bestimmter Merkmalsträger wird in den Daten über die bereitgestellten Gewichtungsvariablen aufgegriffen. Werden diese Gewichtungsvariablen als Gewichtungsanweisung in die Analysekommandos integriert, wird der Einfluss einzelner Merkmalsträger auf die Analyseergebnisse entsprechend seines Repräsentationsfaktors modifiziert. Gewichtete Ergebnisse nicht-repräsentativer Daten bilden also Ergebnisse repräsentativer Daten nach - falls die Gewichte gut sind.
Zusammenhänge zwischen Variablen sind allerdings, anders als Anteilswerte, in der Regel robust gegenüber Abweichungen von der Repräsentativität. Da die in euren Abschlussarbeiten untersuchen Fragen in der Regel auf die Analyse von Zusammenhängen ausgerichtet ist, halten wir die Verwendung von Gewichten in euren Analyse daher nicht für essentiell. Wir stellen euch folglich frei, in Euren Analysen Gewichte zu verwenden oder im Appendix zusätzlich gewichtete Ergebnisse als Robustheitstest zu präsentieren (und in einer Fussnote kurz zu referenzieren). Auch in unserem Beispiel liegen die Ergebnisse einer zusätzlichen gewichteten Analyse sehr eng an den ungewichteten Ergebnissen:
shp_model_weight<-filter(shp_model, w11101_2022>0)
netto3<-lm(lifesat~log(oecd_inc_mon)+educyears+poly(alter, 2, raw=TRUE)+geschlecht+erwerb, shp_model_weight, weights=w11101_2022)
stargazer (netto, netto3, type="text", star.cutoffs = c(.05,.01,.001), column.labels =c("Originalnetto", "Gewichtete Ergebnisse"))##
## ====================================================================
## Dependent variable:
## -----------------------------------
## lifesat
## Originalnetto Gewichtete Ergebnisse
## (1) (2)
## --------------------------------------------------------------------
## log(oecd_inc_mon) 0.342*** 0.301***
## (0.026) (0.026)
##
## educyears 0.0001 -0.001
## (0.004) (0.004)
##
## poly(alter, 2, raw = TRUE)1 -0.012** -0.024***
## (0.004) (0.005)
##
## poly(alter, 2, raw = TRUE)2 0.0002*** 0.0004***
## (0.00004) (0.00005)
##
## geschlechtFemale 0.040 0.115***
## (0.029) (0.029)
##
## erwerbFull Time 0.247***
## (0.044)
##
## erwerbPart Time 0.087* 0.293***
## (0.037) (0.044)
##
## erwerbNot Working -0.098*
## (0.043)
##
## Constant 5.029*** 5.318***
## (0.237) (0.223)
##
## --------------------------------------------------------------------
## Observations 10,495 10,495
## R2 0.035 0.036
## Adjusted R2 0.034 0.035
## Residual Std. Error (df = 10487) 1.390 36.110
## F Statistic (df = 7; 10487) 54.210*** 55.160***
## ====================================================================
## Note: *p<0.05; **p<0.01; ***p<0.001
9 Visualisierung der Regressionsergebnisse
9.1 Visualisierung Haupteffekt
Der Conditional Effect Plot bildet den Verlauf der bereinigten Regressionsfunktion (aus dem Nettomodell) ab - empfehlen wir für jeden Forschungsbeitrag mit regressionsbasierter Analyse. Auch hier gibt es unterschiedliche Workflows; Package unserer Wahl ist derzeit visreg, welches den in diesem Beispiel wichtigen Vorteil hat, dass es per Default die logarithmische Kurve über der linearen Skala (statt der linearen Gerade über der logarithmierten Skala) darstellt.
visreg hält bei der Darstellung der Vorhersagefunktion automatisch die Kovariaten in den Mittelwerten konstant (daher auch conditional effect plot), wodurch der bereinigte Effekt der “durchschnittlichen” Person abgebildet wird. Achtung: Anders als Packages zur Berechnung bedingter vorhergesagter Werte (z.B. emmeans ) stellt visreg dabei nicht auf arithmetische Mittel sondern den Median (bzw. den Modus bei kategorialen Variablen) ab. Durch gg=TRUE die gewohnte ggplot-Funktionalität für die Formatierung der Abbildung verwendet werden:
vis1<-visreg(netto, "oecd_inc_mon", partial=F, rug=F, gg=T)
vis1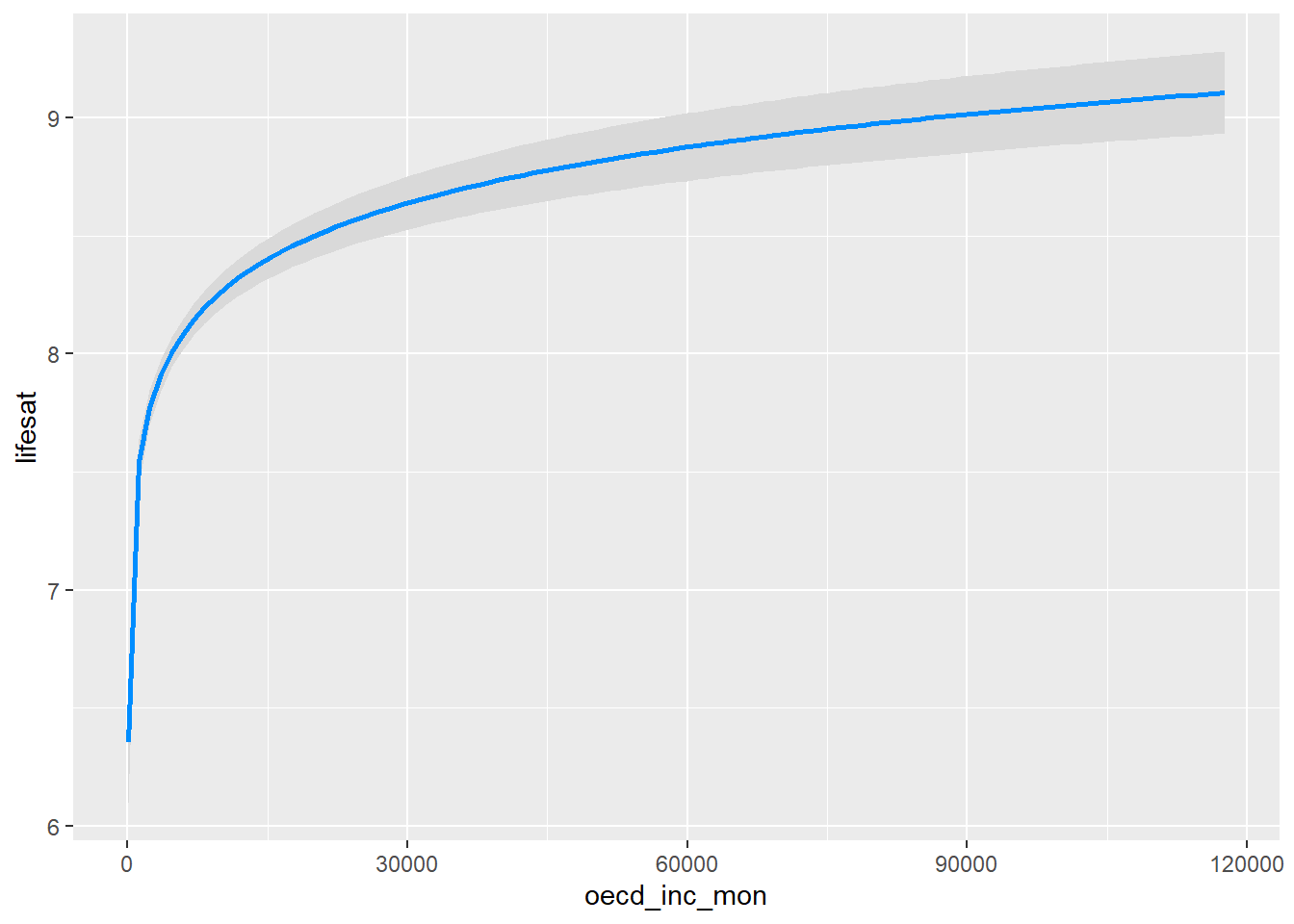
Die Charakteristika des Zusammenhangs und somit die praktischen
Implikationen des ermittelten Koeffizienten werden so sehr schön
deutlich: Der Einfluss des Einkommens auf die Lebenszufriedenheit ist in
niedrigen Einkommensbereichen zunächst sehr stark, flacht aber schon ab
einem monatlichen Einkommen von etwa 2000 Franken deutlich erkennbar und
zunehmend ab. Diesen Charakter der Regressionsfunktion verdeutlichen
auch die auf Basis des Nettomodells vorhergesagten
Werte für eine 35-jährige, vollzeiterwerbstätige Frau:
predict(netto, data.frame(oecd_inc_mon=2000, educyears=12, alter=35, geschlecht="Female", erwerb="Full Time")) ## 1
## 7.537predict(netto, data.frame(oecd_inc_mon=4000, educyears=12, alter=35, geschlecht="Female", erwerb="Full Time")) ## 1
## 7.774predict(netto, data.frame(oecd_inc_mon=6000, educyears=12, alter=35, geschlecht="Female", erwerb="Full Time")) ## 1
## 7.913Steigt ihr Einkommen von 2000 auf 4000 CHF, nimmt die vorhergesagte Lebenszufriedenheit um fast einen viertel Skalenpunkt zu; ein (weiterer) Anstieg von 4000 auf 6000 CHF führt, unter Konstanthaltung der Kovariaten, dann nur noch zu einem Anstieg um etwa einen zehntel Skalenpunkt. Solche eine inhaltliche Interpretationsstrategie, die konditionale Vorhersagen auf Basis der Regressionsschätzung vergleichend einordnet, funktioniert häufig sehr gut im Rahmen von Forschungsberichten oder Präsentationen zur Darstellung der substanziellen Grösse des Koeffizienten bzw. des Effect-Size. Achtung: Wird eine Harmonisierung der abgeleiteten Vorhersagen (bzw. derer Bedingungen) zwischen visreg und predict angestrebt, muss entweder die Kondition im visreg-Befehl auch auf arithmetische Mittel ausgerichtet, oder im predict-Befehl Mediane und Modi abgestellt werden.
Als nächstes trimmen wir die durch visreg erstellte Grafik zur publikationsreife:
vis1+labs(title="Effekt des Einkommens auf die Lebenszufriedenheit",
caption="Vorhergesagte Werte unter Konstanthaltung von Standarddemographie, Bildung und Erwerbstätigkeit (Modell 'Netto') \nSHP v24, n=8987")+
ylab("Lebenszufriedenheit")+
xlab("Monatliches Haushaltsnettoeinkommen")+
coord_cartesian(xlim=c(1500, 20000))+
scale_x_continuous(breaks=seq(2000,20000, 2000))
9.2 Visualisierung Interaktion
visreg eignet sich auch hervorragend zur Visualisierung von Regressionsanalysen mit Interaktionsterm:
vis2<-visreg(moderation, "oecd_inc_mon", by="geschlecht", partial=F, rug=F, gg=T, overlay=T, band=T)
vis2+labs(title="Effektdiagramm mit 95%-CI: Einkommen und Lebenszufriedenheit",
caption="Vorhergesagefunktion (Modell 'Moderation') \nSHP v24, n=8987")+
ylab("Lebenszufriedenheit")+
xlab("Monatliches Haushaltsnettoeinkommen")+
coord_cartesian(xlim=c(2500, 40000), ylim=c(7, 9) )+
scale_x_continuous(breaks=seq(2500, 40000, 5000))+
scale_color_manual(name = "Geschlecht", values = c("Male" = "blue", "Female" = "red"), labels = c("M", "F"))+
guides(fill = FALSE) ## Scale for colour is already present.
## Adding another scale for colour, which will replace the existing scale.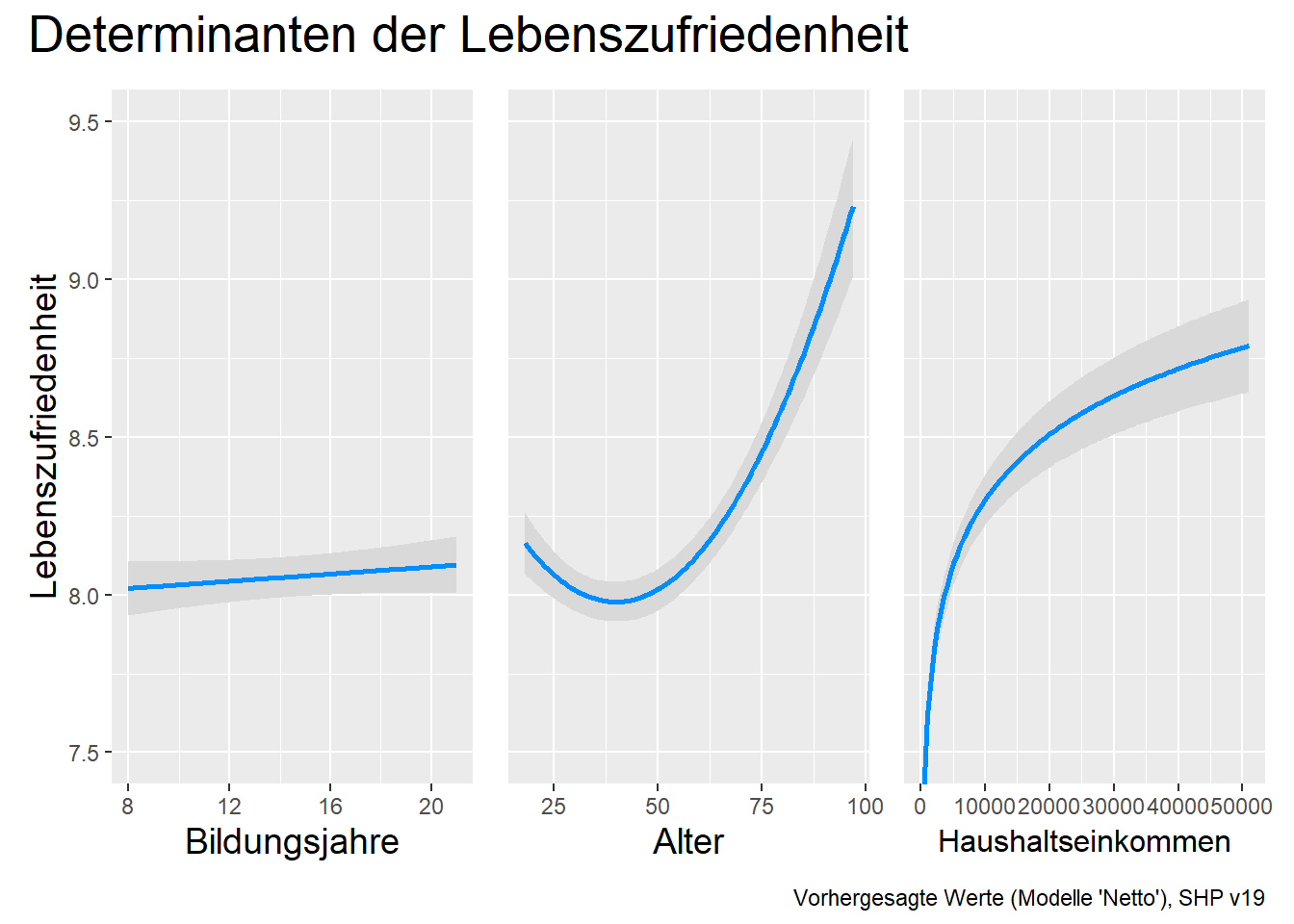
… deutlich wird der geschlechtsspezifisch unterschiedlich starke
Einkommenseffekt, gleichzeitig aber auch die inhaltliche und
statistische Insignifikanz dieser Unterschiede. Der Bildausschnitt wurde
hier so gewählt, dass die Kreuzung der Vorhersagefunktionen
einigermassen gut sichtbar wird. Die Modifikation der Legende ist
herausfordernd und eine Schwäche des Packages, die hier integrierte
Lösung mit scale_color_manual() sollte meistens funktionieren.
9.3 Visualisierung Mediation
Wenn Mediationsprozesse im Fokus des Interesses liegen, kann es hilfreich sein, Netto- und direkten Effekt in einer Abbildung zu kontrastieren - insbesondere, wenn, wie immer häufiger in den Top-Journals praktiziert, die Regressionstabelle in den Anhang abgeschoben wird. Allerdings bieten keine der hier eingeführten Packages diese Funktionalität per Default an. Wenn du eine entsprechende Form der graphischen Aufarbeitung anstrebst, musst du also zunächst manuell Matrizen vorhergesagter Werte generieren, die dann im zweiten Schritt graphisch aufbereitet werden können. Das folgende Beispiel führt diesen Prozess zur Identifikation der Mediationseigenschaften des Wohnungszustandes aus (und illustriert dessen geringe Mediationskraft).
library(ggeffects)
pred_netto <- ggpredict(netto, terms = "oecd_inc_mon [1:40000 by=100]")
pred_mediation <- ggpredict(mediation1, terms = "oecd_inc_mon [1:40000 by=100]", condition = c(zustand = "in good condition but not recently renovated"))
ggplot(pred_netto, aes(x, predicted))+
geom_ribbon(alpha=0.1, aes(ymin=conf.low, ymax=conf.high))+
geom_ribbon(data=pred_mediation, alpha=0.1, fill="deepskyblue", aes(ymin=conf.low, ymax=conf.high))+
geom_line()+
geom_line(data=pred_mediation, aes(x, predicted), color="deepskyblue")+
labs(title="Effektdiagramm mit 95%-CI: Einkommen und Lebenszufriedenheit",
caption="Totaler Effekt (schwarz) und direkter/residualer Effekt (blau), Modelle 'Netto' und 'Mediation') \nSHP v24, n=8987")+
ylab("Lebenszufriedenheit")+
xlab("Monatliches Haushaltsnettoeinkommen")+
coord_cartesian(xlim=c(1500, 20000))+
scale_x_continuous(breaks=seq(2500,20000, 2500))+
theme_bw() 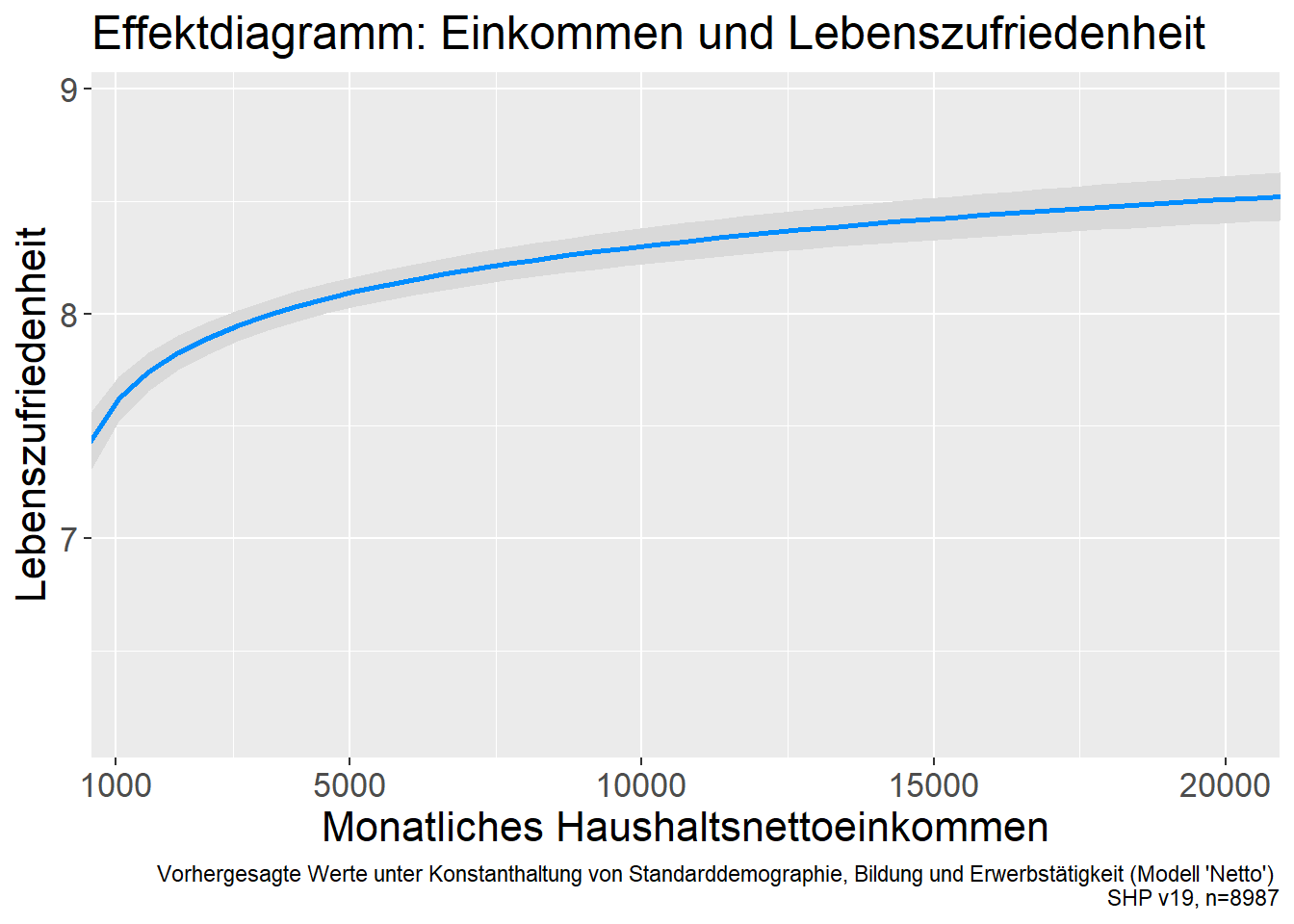
Die blaue Kurve visualisiert nun den residualen bzw. direkten Einkommenseffekt, der nicht über den Wohnungszustand vermittelt wird (= der Einkommenseffekt in einer Welt, in der alle Personen den gleichen guten Wohnungszustand haben).
9.4 Weitere Visualiserungsansätze
Kategoriale UV
vis3<-visreg(netto, "erwerb", partial=F, rug=F, gg=T)
vis3+labs(title="Regressionsfunktion mit 95%-CI: Erwerbstätigkeit und Lebenszufriedenheit",
caption="Vorhergesagte Werte unter Konstanthaltung von Standarddemographie, Bildung und Einkommen (Modell 'Netto') \nSHP v24, n=8987")+
ylab("Lebenszufriedenheit")+
xlab("Erwerbsstatus")
Ein Schwachpunkt von visreg() ist die fehlende
Möglichkeit, Wertelabels im Rahmen des Befehls zu verändern. Dieses
Problem ist hier schon aufgrund der englischen Wertelabel virulent. Die
Anpassung der Wertelabel muss dementsprechend ausserhalb des
Grafikbefehls und noch vor der objektdefinierenden Regressionsanalyse
erfolgen:
shp_model$erwerb <- factor(shp_model$erwerb, labels = c("Full Time" = "Vollzeit", "Part Time" = "Teilzeit", "Not Working" = "Nicht Erwerbstätig"))
netto<-lm(lifesat~log(oecd_inc_mon)+educyears+poly(alter, 2, raw=TRUE)+geschlecht+erwerb, shp_model)
vis3b<-visreg(netto, "erwerb", partial=F, rug=F, gg=T)
vis3b+labs(title="Regressionsfunktion mit 95%-CI: Erwerbstätigkeit und Lebenszufriedenheit",
caption="Vorhergesagte Werte unter Konstanthaltung von Standarddemographie, Bildung und Einkommen (Modell 'Netto') \nSHP v24, n=8987")+
ylab("Lebenszufriedenheit")+
xlab("Erwerbsstatus")
Mehrere UVs (…oder mehrere AVs)
Manchmal ist es sinnvoll, mehrere Abbildungen in einer gemeinsamen Darstellung zusammenzufassen. Dies ist zum Beispiel dann der Fall, wenn die Einflüsse mehrerer unabhängiger Variablen übersichtlich und gemeinsam dargestellt werden sollen, oder wenn wir unsere Hypothese mit mehreren abhängige Variablen testen. Es gibt ein paar R-Packages, die solche multiplen Plots erstellen können. Achtung: Hier können nur grobe Ansätze kurz angerissen werden, die in der Praxis einer Veredelung bedürfen.
Ein relevantes Packager zur Integration mehrere Plots ist ggarrange:
visB1<-visreg(netto, "educyears", partial=F, rug=F, gg=T)
visB2<-visreg(netto, "alter", partial=F, rug=F, gg=T)
visB3<-visreg(netto, "oecd_inc_mon", partial=F, rug=F, gg=T)
library(ggpubr)
figure <- ggarrange(visB1, visB2, visB3,
labels = c("A", "B", "C"),
ncol = 3, nrow = 1)
annotate_figure(
figure,
top = "Determinanten der Lebenszufriedenheit (Modell 'Netto')",
bottom = NULL,
left = NULL,
right = NULL,
fig.lab = NULL,
)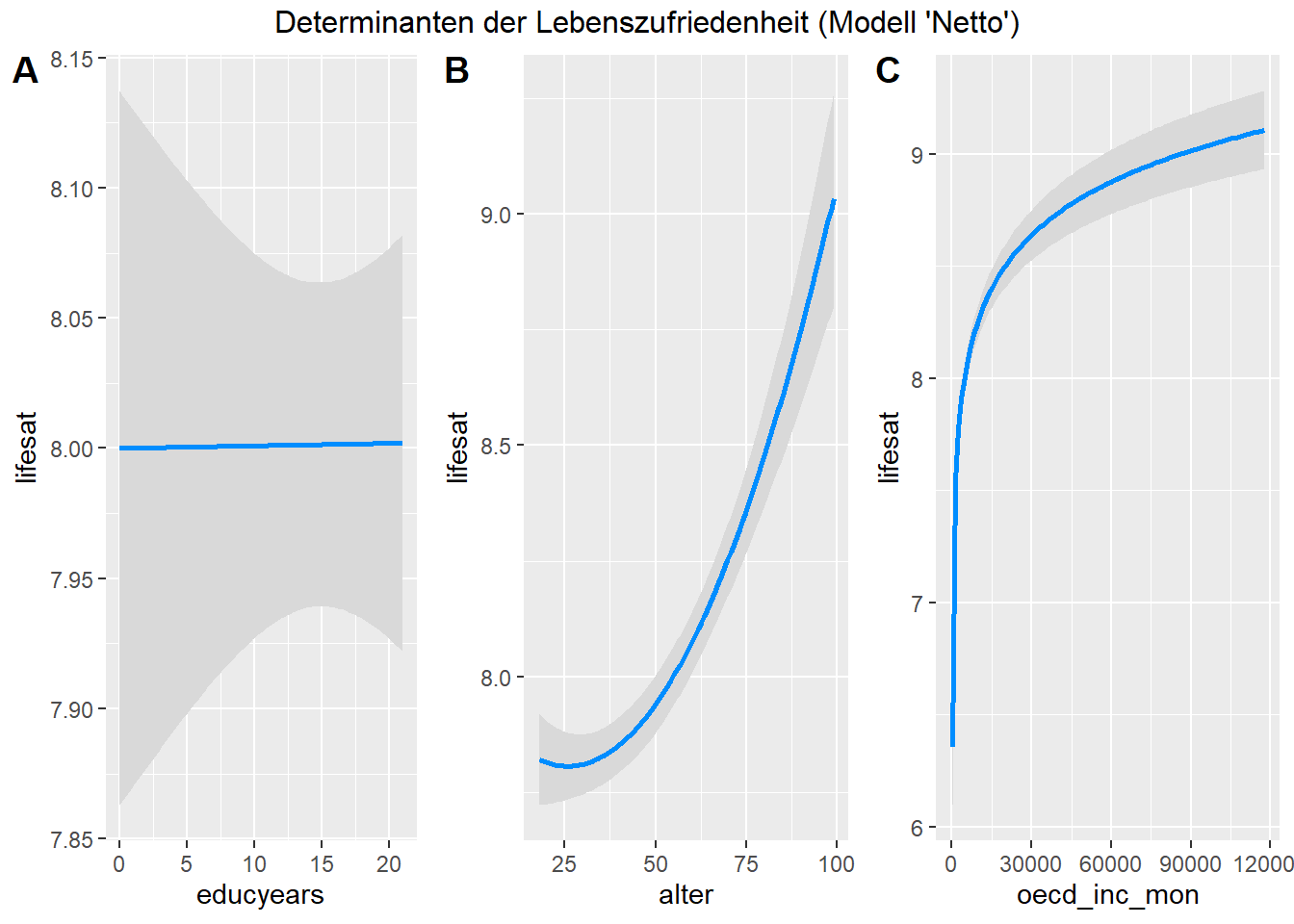
Ein weiteres Package, mit dem ihr mehrere Abbildungen zusammenfügen könnt, ist patchwork. In diesem Codesnippet werden mehrere Lösungen für verschiedene Problemstellungen angedeutet, die häufig im Kontext von multiplen Plots virulent werden.
library (patchwork)
# Füge Achsenlabel & Grössenangaben hinzu und begrenze auf einheitlichen Ausschnitt
visB1 = visB1 + ylab("Lebenszufriedenheit") + xlab("Bildungsjahre")+ coord_cartesian(ylim=c(7.5, 9.5)) + theme(axis.title = element_text(size = 14))
visB2 = visB2 + ylab("Lebenszufriedenheit") + xlab("Alter") + coord_cartesian(ylim=c(7.5, 9.5)) + theme(axis.title = element_text(size = 14))
visB3 = visB3 + ylab("Lebenszufriedenheit") + xlab("Haushaltseinkommen") + coord_cartesian(ylim=c(7.5, 9.5)) + theme(axis.title = element_text(size = 12))
patchwork = visB1 + visB2 + visB3
# Y-Achse muss nur beim ersten Plot gelabelt werden, daher:
# Remove title from second subplot
patchwork[[2]] = patchwork[[2]] + theme(axis.text.y = element_blank(),
axis.ticks.y = element_blank(),
axis.title.y = element_blank() )
# Remove title from third subplot
patchwork[[3]] = patchwork[[3]] + theme(axis.text.y = element_blank(),
axis.ticks.y = element_blank(),
axis.title.y = element_blank() )
# Generiere multiplen plot und definiere übergreifenden titel
patchwork + plot_annotation(title ="Determinanten der Lebenszufriedenheit", caption="Vorhergesagte Werte (Modelle 'Netto'), SHP v24") &
theme(
plot.title = element_text(size = 20) # Increase the size of the title
)
# Speichern/ Exportieren für Publikation (siehe auch unten)
ggsave(filename = "multiplot.png", width = 20, height = 12, dpi=2000, units = "cm")Alternative Darstellung bei mehreren UVs/AVs: Coefficient Plot; https://druedin.com/tag/coefficient-plots/
10 Interpretation
Die tabellarische und grafische Aufbereitung stützt die
Zugänglichkeit der Ergebnisse, ersetzt aber nicht die prosaische
Interpretation. Dabei muss selbst bei einfachen technischen
bzw. Basis-Interpretationen stets anschaulich auf die konkrete
Variable und die konkreten Einheiten Bezug genommen werden -
vermeidet die Begriffe abstrakter, vom Anwendungsfall gelöster
Interpretationsschemata (wie “unabhängige/abhängige Variable”
und “Einheiten”).
Es reicht zudem nicht aus, einfach die
Koeffizienten aus der Tabelle zu zitieren und die statistische
Signifikanz des Ergebnisses zu berichten: die Interpretation
muss vielmehr den Koeffizienten bzw. seine Grösse einordnen und damit
greifbar machen. Einige Anhaltspunkte findet ihr oben in den
jeweiligen Erläuterungen und ad-hoc Interpretationen (z.B. im Abschnitt 5.2), aber grundsätzlich stellt jede
Analyse ihre eigenen Anforderungen, so dass es für die Interpretation
der Regressionskoeffizienten kein pauschales Rezept
gibt. Vielmehr sind (1) statistische Intuition, (2) Einfühlungsvermögen
in eure LeserInnen und (3) eine gedankliche Auseinandersetzung mit Euren
Koeffizienten und deren Bedeutung gefragt. Ein paar Tipps dazu:
- Kernaufgabe ist die Auswertung des Koeffizienten der unabhängigen
Variable aus dem Nettomodell, da dieser die zentrale empirische Aussage
der Studie enthält und ausserdem der Belastung der Hypothese dient.
Koeffizienten der Kontrollvariablen sollten, wenn überhaupt, in einer
kompakten Fussnote zusammenfassend ausgewertet werden.
- Die Standardinterpretation des Regressionskoeffizienten wird oftmals
durch Reskalierung der Bezugseinheit (Interpretation z.B. in 10er oder
1000er Einheiten der UV) deutlich zugänglicher - z.B. bei Einkommens-
oder Altersvariablen
- Grade bei abstrakten Skaleneinheiten ist es häufig hilfreich, in der Interpretation auch mit Standardisierungen zu arbeiten (siehe Beispiele aus unserer Statistik 2 - Veranstaltung).
- Wie oben demonstriert lassen sich insbesondere bei transformierten Variablen die Effekteigenschaften gut durch geeignete Vorhersagepaare verdeutlichen. Dies ist oft auch bei nicht-transformierten Variablen eine hilfreiche Strategie.
- Versucht auch, die Veränderung des zentralen Koeffizienten über die Modelle zu erklären
- Bitte nur am Rande: Auswertung der Koeffizienten der
Kontrollvariablen.
11 Weiterverarbeitung von Grafiken
Einfach, manchmal praktikabel, aber unprofessionell: Der Ad-hoc Ansatz
Aus der R-Konsole heraus können Abbildungen leicht gespeichert, kopiert und weiterverarbeitet werden: Manuell im Plots-Fenster durch verschieben der Fenstergrenzen die Grafik bzw. Seitengrössen und -verhältnisse kalibrieren, dann einfach im “Plots”-tab auf “Export”–>“Image”–>“Save”, schliesslich per Copy & Paste ins Workingpaper oder Präsi. Für ad-hoc Integration z.B. in Präsentationen ist das ein gangbarer Weg. Für “amtliche” Publikationen ist er allerdings aus mehreren Gründen nicht empfehlenswert: Grösse, Schriftgrösse und Auflösung lassen sich kaum aufeinander abstimmen, zudem sind die so produzierten Grafiken kaum replizierbar bzw. reproduzierbar. Spätestens dann, wenn ihr ein Detail verändern wollt oder ihr seitens der Editorenschaft konkrete Vorgaben zur Bildgestaltung und -Formatierung bekommt, fährt der ad-hoc Ansatz vor die Wand.
Der professionelle Ansatz
Für gut kalibrierbare und replizierbare Grafiken empfehlen wir folgende Schritte:
- Nutzt die Optionen zur Definition der Schriftgrössen innerhalb das theme()-Arguments. So könnt ihr ein sinnvolles und über alle Auflösungen konstantes Verhältnis von Plotgrösse und Schriftgrösse herstellen. Empfehlung zum size: Titel etwa 20 (Wenn es seine Länge erlaubt), Achsentitel etwas kleiner, Wertelabel nochmal etwas kleiner - Achtung: Es gibt keine Standardlösung, die immer funktioniert, geht also nicht ohne ausprobieren.
- Speichern der Abbildung z.B. mit ggsave. Dieser Befehl nimmt automatisch Bezug auf die letzte angelegte Grafik. Die Abbildungsdatei befindet sich dann automatisch in eurer Working Directory. Dies ist per Default der Ordner, in dem der Syntax-file gespeichert ist, über den ihr R steuert.
- Spezifikation der Abbildungsattribute und Export mit
ggsave:
- Höhe/Breite: Das relative Verhältnis von Höhe zu Breite
hängt stark von den Eigenschaften Eurer Abbildung sowie der beteiligten
Variablen ab. Die absolute Grösse der beiden Seiten sollte
zwischen 10 und 20 Zentimetern liegen. Sie muss ggf. auf die
Schriftgrösse abgestimmt werden. Auch hier gilt: ohne Probieren geht es
nicht!
- Auflösung: Gegeben der oben vorgeschlagenen Grösse seit ihr für
Präsentationen bei 1000 dpi auf der sicheren Seite. Für Poster braucht
es ggf. noch etwas mehr.
- Format: .png hat sich bewährt, manche empfehlen auch .pdf
- Höhe/Breite: Das relative Verhältnis von Höhe zu Breite
hängt stark von den Eigenschaften Eurer Abbildung sowie der beteiligten
Variablen ab. Die absolute Grösse der beiden Seiten sollte
zwischen 10 und 20 Zentimetern liegen. Sie muss ggf. auf die
Schriftgrösse abgestimmt werden. Auch hier gilt: ohne Probieren geht es
nicht!
vis1b<-vis1+labs(title="Effektdiagramm: Einkommen und Lebenszufriedenheit",
caption="Vorhergesagte Werte unter Konstanthaltung von Standarddemographie, Bildung und Erwerbstätigkeit (Modell 'Netto') \nSHP v24, n=8987")+
ylab("Lebenszufriedenheit")+
xlab("Monatliches Haushaltsnettoeinkommen")+
coord_cartesian(xlim=c(1500, 20000))+
scale_x_continuous(breaks = c(1000, seq(5000, 20000, 5000)) # Specify breaks at 1000, then every 5000 from 5000 to 20000
)+
theme(
plot.title = element_text(size = 18), # Increase title size
axis.title.x = element_text(size = 16), # Increase X axis label size
axis.title.y = element_text(size = 16), # Increase Y axis label size
axis.text.x = element_text(size = 13), # Increase X axis text size
axis.text.y = element_text(size = 13) # Increase Y axis text size
)
vis1b
ggsave(filename = "vis1b.png", width = 20, height = 13, dpi=2000, units = "cm")Der Plot befindet sich nun in Eurem Workingdirektory; ihr könnt ihn direkt über den Tab “files” (rechts unten in der Konsole) ansteuern.
Achtung: Die Parameter in den Funktionen des Befehls müsst ihr meist durch Probieren aufeinander abstimmen. Dies gilt auch für die “theme”-Anweisung im Plotbefehl, mit dem Ihr die Textgrösse passend zum Format ausrichten könnt. Ein Problem ist beispielsweise, dass es keine Option gibt, die Beschriftungsgrösse automatisch an die Ausgabegrösse der Abbildung anzupassen - sie wächst bzw. schrumpft also nicht automatisch mit (sondern muss manuell angepasst werden) wenn ihr die absoluten Seitengrössen eurer Abbildung verändert.
Schlusswort
Die mit dieser Musteranalyse suggerierte und angestrebte Idee einer Rezepthaftigkeit der Datenanalyse soll Euch bei der Analyse zu Eurer Qualifikationsarbeit helfen, widerspricht aber gleichzeitig auch der Konstruktionslogik von R und unserer Programmierrealität: mit dir ist alles in Ordnung, wenn während deiner Datenanalyse nicht die meiste Zeit das R-Fenster geöffnet ist, sondern diverse Foren, Suchmaschinen und kryptische Dokus. Es ist normal, dass du dich nicht gradlinig, sondern in dem Trial-and-Error Modus durch deine Datenanalyse bewegst (der letztlich auch, allerdings weitgehend unsichtbar, hinter diesem Skript steht). Die anwendungsbezogene Auseinandersetzung mit R ist ist eine Art Detektivarbeit, von der dich dieses Muster etwas entlasten, aber nicht entbinden kann.